Crimped fiber composites: mechanics of a finite-length crimped fiber embedded in a soft matrix

Abstract

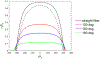
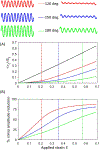
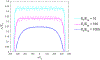
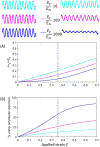
Composites comprising crimped fibers of finite length embedded in a soft matrix have the potential to mimic the strain-hardening behavior of tissues containing fibrous collagen. Unlike continuous fiber composites, such chopped fiber composites would be flow-processable. Here, we study the fundamental mechanics of stress transfer between a single crimped fiber and the embedding matrix subjected to tensile strain. Finite element simulations show that fibers with large crimp amplitude and large relative modulus straighten significantly at small strain without bearing significant load. At large strain, they become taut and hence bear increasing load. Analogous to straight fiber composites, there is a region near the ends of each fiber which bears much lower stress than the midsection. We show that the stress-transfer mechanics can be captured by a shear lag model where the crimped fiber can be replaced with an equivalent straight fiber whose effective modulus is lower than that of the crimped fiber, but increases with applied strain. This allows estimating the modulus of a composite at low fiber fraction. The degree of strain hardening and the strain needed for strain hardening can be tuned by changing relative modulus of the fibers and the crimp geometry.

Keywords: Collagen recruitment; Crimped fiber; Fiber-reinforced composite; Strain hardening.

Fig. 1

(A) Relative dimensions of the matrix and embedded fiber (B) magnified view of the geometry of the fiber, (C) semicircular cross section of the hemicylindrical fiber, (D) examples of how $\theta$ affects the initial amplitude of the fiber, (E) tetrahedral adaptive mesh near the fiber-matrix interface illustrated for the fiber with $\theta ={150}^{\circ }$

Fig. 2

(A) Distribution of ${\epsilon }_f={\sigma }_f/E_f$ for straight fiber: simulation data (black dashed line), Eq. 1 (black solid line), and (B): ${\sigma }_f/E_f$, where ${\sigma }_f$ is the $x$-component of the Cauchy stress in the fiber; for crimped fiber with $\theta ={150}^{\circ }$ : simulation data (blue dashed line), Eq. 6 (blue solid line, discussed in Sect. 5.1). In both graphs, the data are shown at applied strain values (going from top to bottom) of 0.69, 0.51, 0.33, and 0.15. These four values are shown as horizontal dotted black lines in a. The images in $b$ are screenshots of the fiber at the same four strains to illustrate uncrimping

Fig. 3

Distribution of ${\epsilon }_f\left(x\right)={\sigma }_f\left(x\right)/E_f$ for different initial crimp amplitudes given by $\theta =0^{\circ }$ (straight fiber), 120°, 150° and 180°; for $E_f/E_m=1000$ and applied strain = 69% (dashed lines), and Eq. 6 (solid lines, discussed in Sect. 5.1)

Fig. 4

Upper images show amplitude profiles at applied strain $\epsilon =0$ (top left) and $\epsilon =0.69$ (top right). (A) Mean value $⟨{\epsilon }_f⟩$ averaged over two wavelengths near the center, and (B) percent decrease in crimp amplitude in the midportion of the fiber for $E_f=1000$. Vertical lines correspond to the strains needed for geometric straightening (see text)

Fig. 5

Distribution of ${\epsilon }_f\left(x\right)={\sigma }_f\left(x\right)/E_f$ for $E_f=\mathrm{10,100}$ and 1000, and $\theta ={150}^{°}$

Fig. 6

Upper images show amplitude profiles at applied strain $\epsilon =0$ (top left) and $\epsilon =0.69$ (top right). Note that the end-to-end length for profiles on the right are 69% longer than those on the left. (A) Mean value $⟨{\epsilon }_f⟩$ averaged over two wavelengths near the center, and (B) percent decrease in crimp amplitude in the midsection of the fiber for $\theta ={150}^{°}$

Fig. 7

Variation in (A&E) equivalent effective modulus factor $\left.E_f^{e\text{ eff }}/E_f\right)$, (B&F) normalized effective radius $\left(r_f^{\mathit{\text{eff}}}/r_f\right)$, (C&G) normalized effective shear lag length $\left(l_s^{\mathit{\text{eff}}}/r_f\right)$ and (D&H) normalized modulus of the composite $\left(E_{\text{com }}/E_m\right)$ with applied strain using $\varphi =1\times {10}^{-3}$. Left column shows effect of varying crimp amplitude at fixed relative modulus of 1000. Right column shows effect of relative modulus at fixed crimp amplitude corresponding to $\theta ={150}^{°}$. Vertical lines indicate the strains for geometric straightening of the crimps

Fig. 8

Comparison of two different methods of calculating the contribution of single fibers to the force in the composite. Stars show the value of $\beta$ calculated from the end-reaction forces (Eq. A1). Solid lines are calculations of $\alpha$ from the equivalent fiber model (Eq. A2). Dashed black line is the prediction of shear lag model (Eq. A3) with no fitting parameters