An Integrated Approach of Learning Genetic Networks From Genome-Wide Gene Expression Data Using Gaussian Graphical Model and Monte Carlo Method
- PMID: 36865982
- PMCID: PMC9972065
- DOI: 10.1177/11779322231152972
An Integrated Approach of Learning Genetic Networks From Genome-Wide Gene Expression Data Using Gaussian Graphical Model and Monte Carlo Method
Abstract
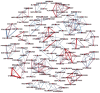
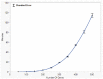
Global genetic networks provide additional information for the analysis of human diseases, beyond the traditional analysis that focuses on single genes or local networks. The Gaussian graphical model (GGM) is widely applied to learn genetic networks because it defines an undirected graph decoding the conditional dependence between genes. Many algorithms based on the GGM have been proposed for learning genetic network structures. Because the number of gene variables is typically far more than the number of samples collected, and a real genetic network is typically sparse, the graphical lasso implementation of GGM becomes a popular tool for inferring the conditional interdependence among genes. However, graphical lasso, although showing good performance in low dimensional data sets, is computationally expensive and inefficient or even unable to work directly on genome-wide gene expression data sets. In this study, the method of Monte Carlo Gaussian graphical model (MCGGM) was proposed to learn global genetic networks of genes. This method uses a Monte Carlo approach to sample subnetworks from genome-wide gene expression data and graphical lasso to learn the structures of the subnetworks. The learned subnetworks are then integrated to approximate a global genetic network. The proposed method was evaluated with a relatively small real data set of RNA-seq expression levels. The results indicate the proposed method shows a strong ability of decoding the interactions with high conditional dependences among genes. The method was then applied to genome-wide data sets of RNA-seq expression levels. The gene interactions with high interdependence from the estimated global networks show that most of the predicted gene-gene interactions have been reported in the literatures playing important roles in different human cancers. Also, the results validate the ability and reliability of the proposed method to identify high conditional dependences among genes in large-scale data sets.
Keywords: Gaussian graphical model; Monte Carlo method; RNA-seq gene expression; gene interaction; genetic network; graphical lasso.
© The Author(s) 2023.
Conflict of interest statement
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Figures
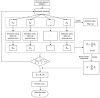
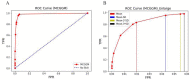
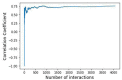
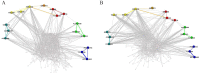

Similar articles
-
Cancer Genetic Network Inference Using Gaussian Graphical Models.Bioinform Biol Insights. 2019 Apr 8;13:1177932219839402. doi: 10.1177/1177932219839402. eCollection 2019. Bioinform Biol Insights. 2019. PMID: 31007526 Free PMC article.
-
An Augmented High-Dimensional Graphical Lasso Method to Incorporate Prior Biological Knowledge for Global Network Learning.Front Genet. 2022 Jan 27;12:760299. doi: 10.3389/fgene.2021.760299. eCollection 2021. Front Genet. 2022. PMID: 35154240 Free PMC article.
-
A linear programming approach for estimating the structure of a sparse linear genetic network from transcript profiling data.Algorithms Mol Biol. 2009 Feb 24;4:5. doi: 10.1186/1748-7188-4-5. Algorithms Mol Biol. 2009. PMID: 19239685 Free PMC article.
-
Pathway Graphical Lasso.Proc AAAI Conf Artif Intell. 2015 Jan;2015:2617-2623. Proc AAAI Conf Artif Intell. 2015. PMID: 26167394 Free PMC article.
-
FastGGM: An Efficient Algorithm for the Inference of Gaussian Graphical Model in Biological Networks.PLoS Comput Biol. 2016 Feb 12;12(2):e1004755. doi: 10.1371/journal.pcbi.1004755. eCollection 2016 Feb. PLoS Comput Biol. 2016. PMID: 26872036 Free PMC article.
Cited by
-
Utilizing systems genetics to enhance understanding into molecular targets of skin cancer.Exp Dermatol. 2024 Mar;33(3):e15043. doi: 10.1111/exd.15043. Exp Dermatol. 2024. PMID: 38459629 Free PMC article. Review.
-
Computational methods in glaucoma research: Current status and future outlook.Mol Aspects Med. 2023 Dec;94:101222. doi: 10.1016/j.mam.2023.101222. Epub 2023 Nov 3. Mol Aspects Med. 2023. PMID: 37925783 Free PMC article. Review.
References
-
- Jensen FV. An Introduction to Bayesian Networks. UCL Press; 1996.
LinkOut - more resources
Full Text Sources

