Robust total X-ray scattering workflow to study correlated motion of proteins in crystals

Abstract

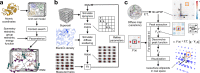
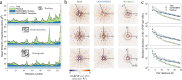
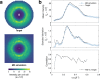
The breathing motions of proteins are thought to play a critical role in function. However, current techniques to study key collective motions are limited to spectroscopy and computation. We present a high-resolution experimental approach based on the total scattering from protein crystals at room temperature (TS/RT-MX) that captures both structure and collective motions. To reveal the scattering signal from protein motions, we present a general workflow that enables robust subtraction of lattice disorder. The workflow introduces two methods: GOODVIBES, a detailed and refinable lattice disorder model based on the rigid-body vibrations of a crystalline elastic network; and DISCOBALL, an independent method of validation that estimates the displacement covariance between proteins in the lattice in real space. Here, we demonstrate the robustness of this workflow and further demonstrate how it can be interfaced with MD simulations towards obtaining high-resolution insight into functionally important protein motions.

Fig. 1. Workflow to measure and interpret protein correlated motion using X-ray crystallography.

First, X-ray diffraction images are acquired from protein crystals at room temperature (RT-MX). The Bragg peaks and continuous scattering are processed separately to obtain the protein structure and a three-dimensional map of diffuse scattering on an absolute intensity scale (electron units). The structure includes mean atomic positions and atomic displacement parameters (ADPs or B-factors) that quantify motion, and the pattern of diffuse scattering depends on how motions are correlated. To separate the internal and external (rigid-body) protein motions, a physical model of lattice disorder is refined to the intense diffuse halo features (GOODVIBES), and the lattice contribution to the diffuse map and variance-covariance matrix of rigid-body motion (V-Cov) are simulated. In parallel, a model-free analysis is performed to estimate displacement covariances (DISCOBALL) and validate the off-diagonal elements of the simulated lattice V-Cov (yellow shading). The lattice contribution to the diffuse map is subtracted and the residual diffuse scattering is sorted by inter-atomic vector using a Fourier transform (3D-ΔPDF). Similarly, the internal ADPs are found by subtracting the lattice contribution (diagonal blocks of V-Cov, blue shading). The internal motion signal can be interpreted by various models. To match crystal simulations, a target diffuse map can be created using GOODVIBES to add back external motions that are consistent with the specific supercell used by the simulations.

Fig. 2. Lattice disorder modeling with GOODVIBES and DISCOBALL.

a Preparation of a rigid-body elastic network model (ENM) for GOODVIBES refinement illustrated using lysozyme in the P2₁2₁2₁ space group. Rigid bodies (white surfaces) are joined by springs with refineable energy functions. The parameterization step enforces space group symmetry and groups springs to avoid overfitting. In this example, springs are grouped according to unique protein-protein interface (sticks colored orange, teal, and purple). b GOODVIBES refinement of the ENM to fit diffuse halos. At each iteration, the variance-covariance matrix of rigid body motion (V-Cov) is computed from the ENM by simulating the thermally-excited vibrations of a large supercell with periodic boundary conditions. The halo scattering profiles are simulated from V-Cov and the electron density of the asymmetric unit, and ENM parameters are refined to improve the fit. c, DISCOBALL algorithm to estimate correlated rigid-body motion of proteins. Peaks are extracted from the 3D-ΔPDF, the Fourier transform (F.T.) of the diffuse map. Each peak, $P_n$, is assumed to be the convolution (*) of the Patterson origin peak, $P\left(r\right)$, and a function that depends on the average joint-ADP ${\mathbf{V}}_n$ of proteins related by a lattice translation operator (integer multiples of lattice vectors). The joint-ADPs are estimated by deconvolution. Joint-ADPs are visualized as iso-probability ellipsoids in real space (blue mesh) to illustrate the anisotropy of each ADP and the overall decay of correlations with protein-protein distance in the crystal (vector from the origin).

Fig. 3. Application of GOODVIBES to experimental datasets from lysozyme polymorphs.

a TS/RT-MX datasets from lysozyme crystallalized in triclinic, orthorhombic, and tetragonal space groups. The unit cells contain one, four, and eight symmetry-related chains, respectively (top row). X-ray diffraction data were acquired at room temperature from multiple large crystals to achieve high signal-to-noise for diffuse mapping (photographs of mounted crystals, middle row). Data were processed to produce three-dimensional maps of diffuse scattering. In the bottom row, the variational component of intensity (total minus isotropic) in electron units ($I_e$) per asymmetric unit (ASU) is shown on a spherical surface at 2 Å resolution, with the positive octant removed to show three central sections. The axes [h,0,0], [0,k,0], and [0,0,l], are colored red, green, and blue, respectively. b GOODVIBES was used to fit a lattice disorder model to each diffuse scattering dataset using supercells shown in the top row. After refinement to a subset of intense halos, the diffuse scattering from lattice disorder was simulated throughout reciprocal space. For all three datasets, GOODVIBES reproduces essential features of the diffuse scattering, as seen for example in central sections (middle vs. bottom row). Blue boxes surround halos included in the fit. The black line is at 2 Å resolution, and axes are drawn as in (a). c For all three datasets, lattice disorder accounts for most of the standard deviation of the intensity in each resolution bin (top row of plots), as well as the precise pattern of intensities as judged by the Pearson correlation coefficient in each resolution shell (bottom row of plots). The correlation approaches the theoretical limit given signal-to-noise of the measurement^, (CC*, black vs. gray lines in the bottom row of plots).

Fig. 4. DISCOBALL analysis and validation of lysozyme polymorph datasets and insight into crystal mechanics.

Displacement covariances matrices (joint-ADPs) were estimated for triclinic, orthorhombic, and tetragonal polymorphs (top to bottom in a–c) and split into total and anisotropic components for further analysis (defined in Methods). a The total covariance from DISCOBALL (blue points) and GOODVIBES (green points) decays with distance between protein molecules, as expected for an elastic crystal. b The GOODVIBES fit shows improved agreement to the total covariances for all polymorphs (Pearson correlations, r, inset). c Validation of GOODVIBES according to the anisotropic components. Anisotropy is especially significant in the orthorhombic crystal (middle panel). d Sections through the orthorhombic crystal are overlaid with isosurface representations of the joint-ADPs from the GOODVIBES model (green mesh) for each protein relative to the asymmetric unit (yellow shading). Correlated motion between nearest neighbors is strong (black arrows) except across the continuous solvent channel running parallel to the a axis (purple shading).

Fig. 5. Contribution of internal protein motion to ADPs and diffuse scattering.

a ADPs of backbone atoms for each lysozyme polymorph (top to bottom: triclinic, orthorhombic, and tetragonal). For clear visualization, the full set of ADPs was reduced to a mean equivalent isotropic B-factor for each residue. Using GOODVIBES, the total B-factor (black line and symbols) is decomposed into rigid-body motion due to lattice disorder (light and dark blue shading) and the residual attributed to internal protein motion (green shading). As described in Methods, the B-factors from rigid-body motion were further decomposed into translations (light blue shading) and rotations (dark blue shading), which vary among residues depending on their distance from the rotation center. The contribution of lattice disorder to B-factors is significant in all three polymorphs, and the residual B-factors have a similar overall magnitude (note that the y-axis scale is different for the triclinic polymorph). b 3D-ΔPDFs computed from the experimental and simulated diffuse maps for each polymorph (arranged top to bottom, as in (a)). Central sections are shown in the a–b plane for the experimental map (left panels), GOODVIBES simulation (middle panels), and the residual after subtraction (right panels), on the same intensity scale normalized per asymmetric unit (ASU). The region near the origin is shown (dashed circle has a radius of 10 Å). c The standard deviation of the full 3D-ΔPDF in shells of constant distance for each map slice shown in (b). Although GOODVIBES and experiment agree at large distances (beyond ~10 Å), a significant residual remains at shorter distances in all three datasets. The rapid decay of the residual component with inter-atomic distance is consistent among the three polymorphs.

Fig. 6. Direct comparison between target diffuse map and crystalline MD.

MD simulations of tetragonal lysozyme were performed on a single unit cell with periodic boundary conditions (PBC) and a 3D diffuse map was simulated. a Slices through 3D maps of total diffuse intensity in the k = 0 plane from MD (bottom panel) and target map derived from experimental data and GOODVIBES fit (top panel) in electron units (I_e) per unit cell. See Methods and Supplementary Fig. 6a for details. b Direct comparison of MD and target diffuse maps in each resolution shell ($1/d$ is the scattering vector magnitude, d is the resolution). The average diffuse intensity (top panel) agrees well between the target (black symbols) and MD (blue symbols). After subtracting the average (see Methods), the standard deviation of intensity is closely matched by MD (middle panel, black vs. blue symbols), including a distinctive shoulder at d ~ 2 Å. The Pearson correlation coefficient (CC, bottom panel) between MD simulation and target diffuse map is best at low resolution ($\text{CC}~$0.8) and decays slightly at high resolution. Source data are provided as a Source Data file.