Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
Randomized Controlled Trial
. 2023 Sep 3;33(5):653-676.
doi: 10.1080/10543406.2023.2170404. Epub 2023 Mar 6.

Practical guidance on modeling choices for the virtual twins method

Chuyu Deng  1 , Jack M Wolf  1 , David M Vock  1 , Dana M Carroll  2 , Jeffrey A Boatman  1 , Dorothy K Hatsukami  3   4 , Ning Leng  5 , Joseph S Koopmeiners  1
Affiliations
Randomized Controlled Trial

Practical guidance on modeling choices for the virtual twins method

Chuyu Deng et al. J Biopharm Stat. .

Abstract

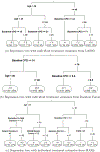
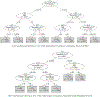
Individuals can vary drastically in their response to the same treatment, and this heterogeneity has driven the push for more personalized medicine. Accurate and interpretable methods to identify subgroups that respond to the treatment differently from the population average are necessary to achieving this goal. The Virtual Twins (VT) method is a highly cited and implemented method for subgroup identification because of its intuitive framework. However, since its initial publication, many researchers still rely heavily on the authors' initial modeling suggestions without examining newer and more powerful alternatives. This leaves much of the potential of the method untapped. We comprehensively evaluate the performance of VT with different combinations of methods in each of its component steps, under a collection of linear and nonlinear problem settings. Our simulations show that the method choice for Step 1 of VT, in which dense models with high predictive performance are fit for the potential outcomes, is highly influential in the overall accuracy of the method, and Superlearner is a promising choice. We illustrate our findings by using VT to identify subgroups with heterogeneous treatment effects in a randomized, double-blind trial of very low nicotine content cigarettes.

Keywords: Virtual twins; causal inference; machine learning; personalized medicine; precision medicine.

PubMed Disclaimer

Figures

Figure A1:
Figure A1:
Resulting trees from VT by using various Step 1 methods, and regression trees for Step 2.
Figure A2:
Figure A2:
Resulting trees from VT by using various Step 1 methods, and conditional inference trees for Step 2.
Figure A2:
Figure A2:
Resulting trees from VT by using various Step 1 methods, and conditional inference trees for Step 2.
Figure 1:
Figure 1:
Overview of the 2 main steps in the Virtual Twins method
Figure 2:
Figure 2:
All the combinations of Step 1 and Step 2 methods we will evaluate in our simulations.
Figure 3:
Figure 3:
Example regression tree with individual treatment estimates from Superlearner
See this image and copyright information in PMC

References

    1. F. J. C., T. J. M.G., and R. S. J., “Subgroup identification from randomized clinical trial data,” Statistics in Medicine, vol. 30, no. 24, pp. 2867–2880, 2011. - PMC - PubMed
    1. Varadhan R, Segal JB, Boyd CM, Wu AW, and Weiss CO, “A framework for the analysis of heterogeneity of treatment effect in patient-centered outcomes research,” Journal of clinical epidemiology, vol. 66, no. 8, pp. 818–825, 2013. - PMC - PubMed
    1. Ilya L, Alex D, and Ralph B, “Tutorial in biostatistics: data-driven subgroup identification and analysis in clinical trials,” Statistics in Medicine, vol. 36, no. 1, pp. 136–196, 2017. - PubMed
    1. Breiman L, “Algorithm cart,” Classification and Regression Trees. California Wadsworth International Group, Belmont, California, 1984.
    1. Athey S, Tibshirani J, and Wager S, “Generalized random forests,” The Annals of Statistics, vol. 47, pp. 1148–1178, Apr. 2019. Publisher: Institute of Mathematical Statistics.

Publication types

LinkOut - more resources