Wigner distribution function approach to analyze MIMO communication within a waveguide

Abstract

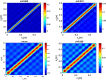
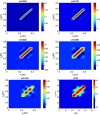
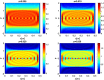
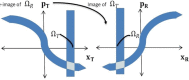
Multiple-input-multiple-output (MIMO) communication is a technology to create high capacity wireless links. The main aim of this paper is to provide a foundation to mathematically model wireless chip to chip communication within complex enclosures. This paper mainly concentrates on modelling wave propagation between transmit and receive antennas through a phase space approach which exploits the relationship between the field-field correlation function (CF) and the Wigner distribution function (WDF). A reliable model of wireless chip-to-chip (C2C) communication helps mitigate the information bottleneck caused due to the wired connections between chips, thus, help improve the efficiency of electronic devices of the future. Placing complex sources such as printed circuit board (PCB) inside a cavity or enclosure results in multi-path interference and hence makes the prediction of signal propagation more difficult. Thus, the CFs can be propagated based on a ray transport approach that predicts the average radiated density, but not the significant fluctuations that occur about it. Hence, the WDF approach can be extended to problems in finite cavities that incorporates reflections as well. Phase space propagators based on classical multi-reflection ray dynamics can be obtained by considering the high-frequency asymptotics.

Keywords: Correlation function; MIMO communication; Waveguide; Wigner distribution function; Wireless C2C communication.

Figure 1

The top figure is a typical open rectangular waveguide where the direction of propagation is along the length of the waveguide. The figure in the bottom mimics the zig-zag propagation inside a waveguide where the ray undergoes total internal reflection at the walls of the waveguide.

Figure 2

Schematic diagram of a two-dimensional system in coordinate space. Σ is the Poincare′ surface of section. x and ${\mathbf{\text{x}}}^{\prime }$ are two points on the Poincare′ surface of section connected by a classical trajectory of one Poincare′ map.

Figure 3

A MIMO set up inside a rectangular waveguide. The transmitting and the receiving antennas are restricted to regions Ω_T and Ω_R respectively. The signals are projected onto the space by the projection operators P_T and P_R.

Figure 4

The figure shows two transmitting and two receiving antennas on a surface with a scatter. α₁,..., α₄ denote the different paths a signal can take between the transmitters and receivers.

Figure 5

Theoretical CFs are shown at the top and bottom for a frequency of 3 GHz at different heights with source at z = 0.005m (top left-hand corner) and propagated to heights z = 0.01m (top right-hand corner), z = 0.02m (bottom left-hand corner) and z = 0.05m (bottom right-hand corner).

Figure 6

Theoretical CFs are shown at the top, middle and bottom rows for a frequency of 3 GHz at different heights with source at z = 0.005m (top left-hand corner) and propagated to heights z = 0.01m (top right-hand corner), z = 0.02m, z = 0.05m (middle row) and z = 0.15m, z = 0.2m (bottom row).

Figure 7

Theoretically obtained WFs are shown along the two rows for a frequency of 3 GHz at different heights with source at z = 0.005m (top left-hand corner) and propagated to heights z = 0.01m (top right-hand corner) and z = 0.02m, z = 0.05m (bottom row) with transmitters and receivers spanning across the width of the waveguide.

Figure 8

The figures shows the phase space density at z = 0 representing the rectangular patch and free space propagation represented by the S-shaped curve for both the domains Ω_T and Ω_R. The phase space density in Ω_T is the pre-image of the phase space density in Ω_R. The shaded region in both the left and right plot corresponds to the region of intersection.

Figure 9

Theoretically obtained WDFs are shown along the four rows for a frequency of 3 GHz at different heights with source at z = 0.005m (top left-hand corner) and propagated to heights z = 0.01m (top right-hand corner), z = 0.02m, z = 0.05m (second row), z = 0.1m, z = 0.15m (third row) and z = 0.2m, z = 0.25m (fourth row) with transmitters and receivers spanning across a small region of the waveguide.