In situ amplification of spin echoes within a kinetic inductance parametric amplifier

Abstract

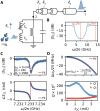
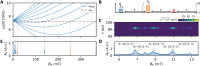
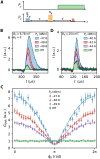
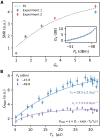
The use of superconducting microresonators together with quantum-limited Josephson parametric amplifiers has enhanced the sensitivity of pulsed electron spin resonance (ESR) measurements by more than four orders of magnitude. So far, the microwave resonators and amplifiers have been designed as separate components due to the incompatibility of Josephson junction-based devices with magnetic fields. This has produced complex spectrometers and raised technical barriers toward adoption of the technique. Here, we circumvent this issue by coupling an ensemble of spins directly to a weakly nonlinear and magnetic field-resilient superconducting microwave resonator. We perform pulsed ESR measurements with a 1-pL mode volume containing 6 × 10⁷ spins and amplify the resulting signals within the device. When considering only those spins that contribute to the detected signals, we find a sensitivity of [Formula: see text] for a Hahn echo sequence at a temperature of 400 mK. In situ amplification is demonstrated at fields up to 254 mT, highlighting the technique's potential for application under conventional ESR operating conditions.

Fig. 1.. Device design and resonator characterization.

(A) Schematic for the device. The resonator is depicted as a lumped element resonator with a geometric inductance (L_g) that couples to an ensemble of ²⁰⁹Bi and a nonlinear inductance L_k, which we exploit for amplification. The resonant mode is confined using a SIF, which we depict as a series of waveguides with alternating Z_hi and Z_lo. (B) Frequency-dependent transmission of the SIF calculated from ABCD matrices. Note that port 2 is used here for illustration and is not physical. The frequencies of the resonator and pump tones are indicated. (C) Frequency-dependent magnitude (top) and phase (bottom) response of the device when measured in reflection (S₁₁) with a vector network analyzer. The solid red lines correspond to a fit of the data in the complex plane, from which we extract the resonator’s parameters. (D) Shift in resonance frequency (top) and variation of the internal and coupling quality factors (bottom) of the device extracted from measurements of S₁₁ made as a function of I_DC. The solid line in the top panel is a fit to the equation in the inset.

Fig. 2.. ESR measurements of²⁰⁹Bi donors in Si using a KIPA.

(A) Allowed ESR transition frequencies for ²⁰⁹Bi in Si as a function of B₀. We can measure ESR with the KIPA when ω_ESR = ω₀, with the crossing points marked by vertical dashed lines. (B) CPMG sequence applied to detect the spins. We use τ = 75 μs and N = 200, averaging the echo produced by each of the N refocusing pulses to increase the SNR. (C) Homodyne-demodulated signal in the time domain as a function of B₀, measured with the CPMG sequence shown in (B). The bright features correspond to a spin echo signal. (D) Integrated spin echo signal from (C). We label the five peaks according to the ESR transitions we expect from calculations of the spin Hamiltonian. a.u., arbitrary units. (E) Measurements of the S_x transitions between 0 and 370 mT. Each measurement is independently normalized.

Fig. 3.. Degenerate amplification of spin echoes.

(A) A modified Hahn echo pulse sequence where a strong parametric pump at frequency ω_p = 2ω₀ and power P_p is supplied following the refocusing pulse. The device functions as a typical high-Q resonator for the first half of the pulse sequence and as a degenerate parametric amplifier during the period the spins induce a signal in the device. (B) Amplified spin echoes measured along the I-quadrature for several P_p. For these measurements, ϕ_p = 0, I_DC = 3.0 mA, and B₀ = 6.78 mT. The data are normalized to the measurement with the pump off. (C) G_SNR measured at the same set point as in (B). The improvement to the SNR is ϕ_p dependent because the amplifier is operated in degenerate mode. The error bars correspond to the SEM, and the solid lines are guides to the eye. (D) Amplified spin echoes measured with I_DC = 2.0 mA and B₀ = 254 mT. Note that at this set point, we average measurements over the pump phase ϕ_p. The data are normalized to the measurement with the pump off.

Fig. 4.. SNR gain and amplifier bandwidth.

(A) SNR measured as a function of G_k. The dashed line is a fit of the data to a model derived from cavity input-output theory (see the Supplementary Materials). Experiments 1 and 2 are equivalent experiments performed on different days. The data for experiment 2 were scaled by a factor of 1.33 so that the SNR with the pump off matches experiment 1. Inset: G_k measured as a function of P_p. (B) G_SNR measured as a function of T_e. The solid lines are fits to the equation in the inset.

Fig. 5.. The BA and comparison with the resonant Δ=0 regime of operation.

(A) Reflection magnitude response measured at different probe frequencies ω/2π for increasing pump amplitude $\sqrt{P_{\mathrm{p}}}$ applied at ω_p/2π = 14.3775 GHz (i.e., Δ/2π = 2.5 MHz). Data taken at I_DC = 3 mA. As $\sqrt{P_{\mathrm{p}}}$ is increased, two features are observed, one below ω_p/2 showing an increasing positive gain peak and another centered at the cavity resonance ω₀ showing a dip, indicating that the resonator is operating close to critical coupling. The two features merge at high pump amplitude where the gain is maximum. (B) Selected traces at four different $\sqrt{P_{\mathrm{p}}}$ for Δ/2π = 2.5 MHz (blue traces, ω_p/2π = 14.3775 GHz) and Δ/2π = 0 (red traces, ω_p = 2ω₀). The red traces are shifted by 2 to 4 MHz to align the amplification features with equivalent gain. Inset: Extracted bandwidths (BW) (plot on a logarithmic scale) for both amplification modes of operation in the main panel. Red squares correspond to the resonant (Δ = 0) configuration, and blue circles correspond to the BA. Additional data points are included in the inset that are not shown in the main panel. For gains larger than 5 dB, the amplification bandwidth can be enhanced by more than an order of magnitude when operated in the BA mode.