Harmonic-Gaussian Symmetric and Asymmetric Double Quantum Wells: Magnetic Field Effects

Abstract

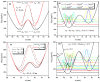
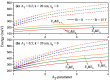
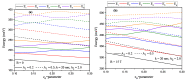
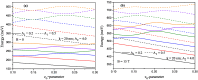
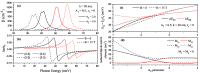
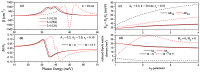
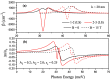
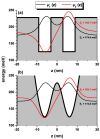
In this study, we considered the linear and non-linear optical properties of an electron in both symmetrical and asymmetrical double quantum wells, which consist of the sum of an internal Gaussian barrier and a harmonic potential under an applied magnetic field. Calculations are in the effective mass and parabolic band approximations. We have used the diagonalization method to find eigenvalues and eigenfunctions of the electron confined within the symmetric and asymmetric double well formed by the sum of a parabolic and Gaussian potential. A two-level approach is used in the density matrix expansion to calculate the linear and third-order non-linear optical absorption and refractive index coefficients. The potential model proposed in this study is useful for simulating and manipulating the optical and electronic properties of symmetric and asymmetric double quantum heterostructures, such as double quantum wells and double quantum dots, with controllable coupling and subjected to externally applied magnetic fields.

Keywords: double quantum well; harmonic-Gaussian potential; magnetic field.

Figure 1

Harmonic-Gaussian DQW confinement potential profile for a constant value of $k=20$ nm versus the z-growth direction coordinate. Harmonic-Gaussian symmetric DQW, solid (dashed) lines are for $A_2=2.0$ ($A_2=4.0$) and black (red) lines $A_1=0.2$ ($A_1=0.5$) (a). For $z_0=0.15$, $A_1=0.5$, and $A_2=2.0$ harmonic-Gaussian asymmetric DQW confinement profile and squared wave functions corresponding to the first six energy levels (b). For different $z_0$-values and some values of the structure parameters, the harmonic-Gaussian asymmetric DQW profile (c), and harmonic-Gaussian asymmetric DQW confinement profile and squared wave-functions corresponding to the first six energy levels for the constant values of $A_2$ and $z_0$ but two different values of the parameter-$A_1$ (d).

Figure 2

For $k=20\mathrm{nm}$ and $z_0=0$, the variation of the energies corresponding to the first six lower-lying levels of a confined electron within Harmonic-Gaussian symmetric DQW as a function of the $A_2$-parameter: $A_1=0.2$ (a) and $A_1=0.5$ (b). Solid (dashed) lines are for $B=0$ ($B=15\mathrm{T}$).

Figure 3

For $A_2=2.0$, the variation of the energies that corresponds to the first six lower-lying levels of a confined electron within Harmonic-Gaussian asymmetric DQW as a function of the $z_0$-parameter. Solid (dashed) lines are for $A_1=0.2$ ($A_1=0.5$). Results are for $B=0$ (a) and $B=15\mathrm{T}$ (b).

Figure 4

Results are as in Figure 3, but for $A_2=4.0$.

Figure 5

For some transitions between the energy levels in harmonic-Gaussian symmetric DQW ($z_0=0$) with $A_1=0.5$, the variation of total absorption coefficients as a function of the incident photon energy (a) and the variation of total refractive index as a function of the incident photon energy (b). Here, black (red) lines are for $A_2=2.0$ ($A_2=4.0$), according to parameter-$A_2$. The variation of the energy difference between related levels (c) and the variation of reduced dipole matrix element (d), where black/red lines are for (2–3)/(2–4) transitions. Solid (dashed) lines are for $B=0$ ($B=15\mathrm{T}$).

Figure 6

For some transitions between the energy levels in harmonic-Gaussian asymmetric DQW with $z_0=0.10$, $A_1=0.2$, and $A_2=2.0$, the variation of total absorption coefficients as a function of the incident photon energy (a), the variation of total refractive index as a function of the incident photon energy (b). According to the parameter-$A_2$, the variation of the energy difference between related levels (c) and the variation of reduced dipole matrix element (d), where black/red lines are for (1–3)/(2–4) transitions. Solid (dashed) lines are for $B=0$ ($B=15\mathrm{T}$).

Figure 7

For some transitions between the energy levels in Harmonic-Gaussian asymmetric DQW with $z_0=0.25$, $A_1=0.2$, and $A_2=2.0$, the variation of total absorption coefficients as a function of the incident photon energy (a) and the variation of total refractive index as a function of the incident photon energy (b). Solid (dashed) lines are for $B=0$ ($B=15\mathrm{T}$).

Figure 8

The ground and the first excited states wave functions for a confined electron in rectangular shaped (a) and harmonic-Gaussian (b) symmetric double quantum wells. The corresponding energies are also depicted.