Identifying regulation with adversarial surrogates
- PMID: 36920920
- PMCID: PMC10041131
- DOI: 10.1073/pnas.2216805120
Identifying regulation with adversarial surrogates
Abstract
Homeostasis, the ability to maintain a relatively constant internal environment in the face of perturbations, is a hallmark of biological systems. It is believed that this constancy is achieved through multiple internal regulation and control processes. Given observations of a system, or even a detailed model of one, it is both valuable and extremely challenging to extract the control objectives of the homeostatic mechanisms. In this work, we develop a robust data-driven method to identify these objectives, namely to understand: "what does the system care about?". We propose an algorithm, Identifying Regulation with Adversarial Surrogates (IRAS), that receives an array of temporal measurements of the system and outputs a candidate for the control objective, expressed as a combination of observed variables. IRAS is an iterative algorithm consisting of two competing players. The first player, realized by an artificial deep neural network, aims to minimize a measure of invariance we refer to as the coefficient of regulation. The second player aims to render the task of the first player more difficult by forcing it to extract information about the temporal structure of the data, which is absent from similar "surrogate" data. We test the algorithm on four synthetic and one natural data set, demonstrating excellent empirical results. Interestingly, our approach can also be used to extract conserved quantities, e.g., energy and momentum, in purely physical systems, as we demonstrate empirically.
Keywords: artificial neural networks; biological control; biological regulation; computational biology; data analysis.
Conflict of interest statement
The authors declare no competing interest.
Figures
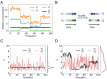

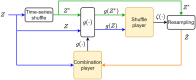



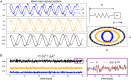

References
-
- Hsiao V., Swaminathan A., Murray R. M., Control theory for synthetic biology: Recent advances in system characterization, control design, and controller implementation for synthetic biology. IEEE Control Syst. Magaz. 38, 32–62 (2018).
-
- El-Samad H., Biological feedback control-respect the loops. Cell Syst. 12, 477–487 (2021). - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

