Building insightful, memory-enriched models to capture long-time biochemical processes from short-time simulations

Abstract

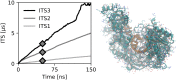
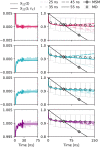
The ability to predict and understand complex molecular motions occurring over diverse timescales ranging from picoseconds to seconds and even hours in biological systems remains one of the largest challenges to chemical theory. Markov state models (MSMs), which provide a memoryless description of the transitions between different states of a biochemical system, have provided numerous important physically transparent insights into biological function. However, constructing these models often necessitates performing extremely long molecular simulations to converge the rates. Here, we show that by incorporating memory via the time-convolutionless generalized master equation (TCL-GME) one can build a theoretically transparent and physically intuitive memory-enriched model of biochemical processes with up to a three order of magnitude reduction in the simulation data required while also providing a higher temporal resolution. We derive the conditions under which the TCL-GME provides a more efficient means to capture slow dynamics than MSMs and rigorously prove when the two provide equally valid and efficient descriptions of the slow configurational dynamics. We further introduce a simple averaging procedure that enables our TCL-GME approach to quickly converge and accurately predict long-time dynamics even when parameterized with noisy reference data arising from short trajectories. We illustrate the advantages of the TCL-GME using alanine dipeptide, the human argonaute complex, and FiP35 WW domain.

Keywords: Markov state models; biomolecular dynamics; generalized master equations; memory effects; protein folding.

Fig. 1.

Application of the TCL-GME to alanine dipeptide with comparisons to the MSM and qMSM (A) Root mean square error (RMSE) curves for the MSM, qMSM, and TCL-GME quantifying the deviation from the MD data (open circles) as the model is parameterized with increasing amounts of data (RMSE Analysis). Vertical lines show the errors associated with cutoffs (τ) of 1.5 ps and 10 ps. Alanine dipeptide is shown (2 residues). (B) State 1 TPM dynamics, ${\mathcal{C}}_{11}(t)$, computed with MSM, qMSM, and TCL-GME approaches parameterized with 1.5 ps of MD data, i.e., τ_L = τ_K = τ_R = 1.5 ps. (C) State 1 TPM dynamics computed with τ_L = τ_K = τ_R = 10 ps. The 4-state TPMs parameterized with τ_K = τ_R = 1.5 ps and τ_L = 10 ps are shown in SI Appendix, Fig. S1. MD error bars were obtained using a bootstrapping approach as discussed in ref. .

Fig. 2.

Demonstration that the massive spatial and temporal scales of the argonaute protein present a challenge to MSMs. Left: Implied timescales (ITS) plot of Eq. 3, for the three nonunitary eigenvalues, whose plateau time corresponds to the Markovian lag time, τ_L. Diamonds show the choice of τ_L in Fig. 3, but one can appreciate that no choice for this window of MD data would be satisfactory. Using the $⟨\mathcal{U}⟩$-GME approach (discussed in this section), Markovianity is found to require ∼1, 200 times as much simulation data. Right: Rendering of the argonaute protein containing the mRNA strand used to obtain the MD data. The protein itself is composed of 831 residues.

Fig. 3.

Instability of the qMSM and TCL-GME in the case of the argonaute protein and demonstration of the robustness of our $⟨\mathcal{U}⟩$-GME approach. (A) The transparent line shows the state 2 memory kernel ${\mathcal{K}}_{22}(t)$ as a function of time. From the RMSE SI Appendix, Fig. S2A, we observe that $\mathcal{K}(t)$ converges by 35 ns. The solid line shows the replacement of ${\mathcal{K}}_{22}(t)$ with zero after this time. (B) Time-dependent conditional probability of starting in state 2 and remaining in state 2 (state 2 dynamics) predicted using the qMSM with τ_K ∈ {25, 35, 45, 55} ns, where increasing transparency corresponds to decreasing values of τ_K. (C) Similar to (A), the transparent line shows the state 2 time-local generator ${\mathcal{R}}_{22}(t)$ as a function of time, and the solid line shows the replacement of $\mathcal{R}(t)$ with $\mathcal{R}({\tau }_R)$ after τ_R = 30 ns. (D) State 2 dynamics predicted using the TCL-GME with τ_R ∈ {25, 35, 45, 55} ns, where increasing transparency corresponds to decreasing values of τ_R. (E) Like (C), the transparent line shows ${\mathcal{R}}_{22}(t)$ as a function of time. Here, the solid line is instead illustrating the replacement of $\mathcal{R}(t)$ with its time average over the window [20, 30] ns after τ_R = 30 ns, i.e., (t_r, τ_R)=(20, 30) ns. (F) Dynamics predicted using the $⟨\mathcal{R}⟩$-GME. (G) The transparent line shows propagator ${\mathcal{U}}_{22}(t)$ as a function of time, and the solid line shows the replacement of $\mathcal{U}(t)$ with its average over the window [20, 30] ns after τ_R = 30 ns. (H) Dynamics predicted using the $⟨\mathcal{U}⟩$-GME. In (B), (D), (F), and (H), we show an MSM parameterized with τ_L = 50 ns. The MD data and error bars were computed using the bootstrapping approach (ref. for details).

Fig. 4.

Ability of our $⟨\mathcal{U}⟩$-GME to accurately predict the dynamics of the FiP35 WW domain. (A) RMSE curves for the MSM and the $⟨\mathcal{U}⟩$-GME as a function of τ_L and τ_R, while varying choices of t_r to illustrate convergence. The structure of the FiP35 WW domain is shown (35 residues). (B) TPM dynamics (${\mathcal{C}}_{22}(t)$) computed using $⟨\mathcal{U}⟩$-GME and MSM approaches with τ_R = 25 ns (ℓ = 5 ns) and τ_L = 25 ns. (C) The propagator ${\mathcal{U}}_{22}(t)$ as a function of time, showing that $\mathcal{U}$ has been replaced with its average at 25 ns.