Non-Abelian effects in dissipative photonic topological lattices

Abstract

Topology is central to phenomena that arise in a variety of fields, ranging from quantum field theory to quantum information science to condensed matter physics. Recently, the study of topology has been extended to open systems, leading to a plethora of intriguing effects such as topological lasing, exceptional surfaces, as well as non-Hermitian bulk-boundary correspondence. Here, we show that Bloch eigenstates associated with lattices with dissipatively coupled elements exhibit geometric properties that cannot be described via scalar Berry phases, in sharp contrast to conservative Hamiltonians with non-degenerate energy levels. This unusual behavior can be attributed to the significant population exchanges among the corresponding dissipation bands of such lattices. Using a one-dimensional example, we show both theoretically and experimentally that such population exchanges can manifest themselves via matrix-valued operators in the corresponding Bloch dynamics. In two-dimensional lattices, such matrix-valued operators can form non-commuting pairs and lead to non-Abelian dynamics, as confirmed by our numerical simulations. Our results point to new ways in which the combined effect of topology and engineered dissipation can lead to non-Abelian topological phenomena.

Fig. 1. Network of time-multiplexed resonators.

a Schematic diagram of the experimental setup used to implement dissipatively coupled resonators. An intensity modulator (IM) and a phase modulator (PM) are used in the input of the optical fiber to generate arbitrary wavefunctions defined by injected femtosecond pulses from a mode-locked laser with a repetition rate of T_R. An Erbium-doped fiber amplifier (EDFA) is used in the main cavity to compensate for the losses and increase the number of measurement roundtrips. Two delay lines with smaller and larger lengths than the main cavity (corresponding to delays of − T_R and + T_R, respectively) are used to dissipatively couple the pulses. b Schematic of a resonant cavity loop (yellow) which hosts N pulses, each representing a resonator element in a dissipatively-coupled lattice. The delay lines (shown in green) provide the dissipative couplings with different rates between nearest-neighbor sites.

Fig. 2. Experimental demonstration of Bloch oscillations in a uniform, dissipatively-coupled open lattice.

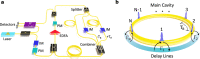
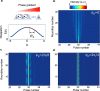
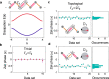
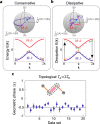
a Applying a phase gradient among the pulses in the time-multiplexed network transports the associated Bloch eigenstates in the reciprocal space by a value of δk = ϕ₀ per cavity roundtrip, where ϕ₀ denotes the pulse-to-pulse phase differences induced by the intracavity phase modulator. b to d, Pulse intensity measurements associated with ϕ₀ = 0, 2π/8 and 2π/4, respectively. In all cases, optical power is initially launched into one lattice element (pulse number 32). As shown in b, in the absence of the effective force (ϕ₀ = 0) light undergoes dissipative discrete diffraction in the lattice. In contrast, when a nonzero phase gradient is established among the pulses, optical power exhibits an oscillatory pattern with a Bloch period equal to N_B = 8, 4 in c, d, respectively. In all cases, the optical power across the lattice sites is normalized in every round trip to provide a more distinct visualization of the field intensities.

Fig. 3. Measuring the geometric Zak phase in a dissipative SSH model using dissipative Bloch oscillations.

a Schematic diagram of an SSH lattice with two different couplings Γ_A = 2Γ_B together with its associated dissipation bands. Since the interactions among the constituent elements are arising from the corresponding dissipators, these bands represent relative gain/decay rates, with the upper-band Bloch eigenstates experiencing relative gain while the ones associated with the lower band decay faster. b–d Experimentally measured Zak phases under various coupling conditions. A trivial coupling between the lattice sites Γ_A = Γ_B leads to a zero Zak phase b. On the other hand, when the intercell and intracell dissipators differ, our measurements show ϕ_Z1 ≈ 0.47π and ϕ_Z2 ≈ − 0.51π for the two possible dimerizations D₁ and D₂ shown in c, d, respectively. These nontrivial phases are geometrically equivalent to the counter-clockwise and clockwise windings of the upper-band Bloch eigenstates on the associated Bloch sphere, as depicted in the insets c, d, respectively. Each data set represents various unit cells (shown in dashed lines) within a single measurement, except for the two first and last units to avoid edge effects. In all cases the error bars indicate standard deviations.

Fig. 4. Modified geometric phases in the presence of non-Abelian effects.

a Geometric winding of the lower-band Bloch eigenstates associated with a conservative SSH Hamiltonian illustrated on the Bloch sphere. In this representation, the upper and lower Bloch eigenstates are located on the equatorial plane, shown in red and blue colors, respectively. Here, $\left.∣A\right)⟩$ and $\left.∣B\right)⟩$ represent the uniformly distributed states residing on the A and B sublattices, corresponding to the points located on the south and the north poles of the Bloch sphere, respectively. The magenta and light blue arrows represent the upper- and lower-band Bloch eigenstates associated with the Bloch momentum k = 0, respectively. The lower panel indicates reciprocal-space dynamics associated with the lower band, which in the adiabatic regime is independent of the upper band. b Similar results for a dissipative SSH Lindbladian are obtained from the corresponding modified Wilson line operator (Eq. (2)). Unlike the conservative case a, the lower-band of a dissipative SSH lattice is expected to exhibit a different geometric phase than that of the upper one. This is because the dissipation bands emerging in the latter are coupled via the off-diagonal Wilczek-Zee connections (A_pq), as illustrated in the lower panel b. Hence, during a Bloch period, the upper-band eigenstates (represented by green dots) are relatively amplified while those associated with the lower one (shown as orange dots) experience a higher attenuation. Eventually, the state of the system at the end of this cycle is determined by the interference between the eigenstates associated with these two bands, which is dominated by the upper-band contribution. This results in a π phase shift in the lower-band geometric phase. The left and right black dotted arrows represent the transfer of Bloch eigenstate populations from the lower band to the upper one and vice versa, respectively. c Experimentally measured values (to be compared with Fig. 3c) indeed corroborate these theoretical predictions. In all cases the error bars indicate standard deviations.

Fig. 5. Non-Abelian dynamics involving Bloch eigenstates in a dissipative honeycomb lattice.

a Schematic of a dissipative honeycomb lattice with two sublattices A and B. b Dissipation bands associated with the Bloch eigenstates of the lattice. c The Brillouin zone in the reciprocal space where an initial point at k = k₀ is shown together with two different closed loops C₁ and C₂ along which the initial state is transported. d Simulation results displaying the initial and final states on the Bloch sphere clearly show the non-commutative nature of the modified Wilson lines defined in Eq. (2), $\widehat{{\mathit{W}}^{\prime }}\left(C_1\right)\widehat{{\mathit{W}}^{\prime }}\left(C_2\right)\ne \widehat{{\mathit{W}}^{\prime }}\left(C_2\right)\widehat{{\mathit{W}}^{\prime }}\left(C_1\right)$.