Synergies of Multiple Zeitgebers Tune Entrainment

Abstract

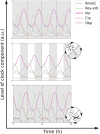
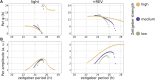
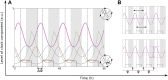
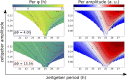
Circadian rhythms are biological rhythms with a period close to 24 h. They become entrained to the Earth's solar day via different periodic cues, so-called zeitgebers. The entrainment of circadian rhythms to a single zeitgeber was investigated in many mathematical clock models of different levels of complexity, ranging from the Poincaré oscillator and the Goodwin model to biologically more detailed models of multiple transcriptional translational feedback loops. However, circadian rhythms are exposed to multiple coexisting zeitgebers in nature. Therefore, we study synergistic effects of two coexisting zeitgebers on different components of the circadian clock. We investigate the induction of period genes by light together with modulations of nuclear receptor activities by drugs and metabolism. Our results show that the entrainment of a circadian rhythm to two coexisting zeitgebers depends strongly on the phase difference between the two zeitgebers. Synergistic interactions of zeitgebers can strengthen diurnal rhythms to reduce detrimental effects of shift-work and jet lag. Medical treatment strategies which aim for stable circadian rhythms should consider interactions of multiple zeitgebers.

Keywords: circadian clock; mathematical model; resonance; synchronisation; zeitgeber synergy.

FIGURE 1

Sketches of the two investigated mammalian clock models. (A) Transcriptional translational feedback loops of the modified Korenčič model. (B) Gene-regulatory network of the Almeida model (Almeida et al., 2020b).

FIGURE 2

Time traces of the modified Korenčič model in constant darkness (DD) (top), 12:12 light-dark cycles (LD) (middle, grey bars indicate the dark phase) and 12:12 drug—no drug cycles (bottom, drug presence visualised as square wave). Both zeitgebers result in successful entrainment to a period of 24 h. The simulation of a Rev-Erbα agonist (+REV) was chosen as drug. For the equations and parameter values of the simulations Supplementary Equation S1-1. All plots show Bmal1 _x , Rev−erb _x , Per _x , Cry _x , and DBP _x .

FIGURE 3

Entrainment to solitary zeitgebers in the modified Korenčič model, the zeitgeber period controls the phase of entrainment (A) and the entrained amplitude (B). The free running period of the model is 24.8 h. Per φ denotes the phase of entrainment. The chosen zeitgeber strengths are r _light = (0.1, 0.2, 0.4) and r _+REV = (0.1, 0.2, 0.4).

FIGURE 4

(A) Time traces of the modified Korenčič model, which is entrained to two coexisting zeitgebers with periods of 24 h. Dark phases are indicated via grey bars and drug level is shown as square wave. There is a phase difference ΔΦ = 6 h between zeitgeber onsets. (B) The small graphs illustrate the frequency locking at a period of 24 h (black horizontal arrows), the resulting amplitude of Per (pink vertical arrow) and the phase φ (black vertical arrows) which is measured when the rising Per level is crossing the mean Per level. Light is turned on within the white bars. The solid, black vertical line highlights the onset of light. Dashed, black vertical lines highlight the onset of drug presence. Colours of the clock components are given in Figure 2.

FIGURE 5

Entrainment of the modified Korenčič model to two coexisting zeitgebers (light and REV agonist) with equal zeitgeber periods. The phase differences between zeitgeber onsets ΔΦ is varied. For ΔΦ = 12 h we find a zeitgeber synergy resulting in a broad range of entrainment which is accompanied by amplitude resonance. For ΔΦ = 3 h there is a smaller range of entrainment.

FIGURE 6

(A) The phase difference ΔΦ between the zeitgebers is varied in 1-h steps in the modified Korenčič model. Squares indicate the resulting entrainment phases and amplitudes. (B) Illustration of antagonistic (blue arrows) and synergistic effects (red arrows), also indicated by larger amplitudes. (C) The modified Korenčič model entrains differentially to varied amplitudes depending on the phase difference between the two zeitgebers. Note the early onset of entrainment at r = 0.1 for the optimal phase difference ΔΦ = 15.5 h (D) Entrained phases lock relative to the light onset or follow the alterations in drug onset dependent on ΔΦ in the Almeida model, some ΔΦ result in period doubling (additional yellow squares). Note that we chose to display Per for the modified Korenčič model but E4BP4 for the Almeida model because these are the clock components with the largest amplitudes. Both zeitgebers have periods of 24 h r _light = 0.2 and r _+REV = 0.2 in (A,B). r _light = r _+REV are varied in (C). r _light = 4.0, r _+REV = 0.04 in (D). Yellow bars indicate light and blue bars indicate drug presence.

FIGURE 7

Arnold-tongues of the modified Korenčič model at synergistic (ΔΦ = 15.5 h) and antagonistic (ΔΦ = 4 h) zeitgeber differences. Both zeitgebers have the same zeitgeber periods and the same zeitgeber amplitudes r _light = r _+REV . Within the region of the Arnold tongue, which is coloured according to phase of entrainment (left plots) or entrained amplitude (right plots), there is successful entrainment with a 1:1 period ratio of zeitgeber and circadian rhythm. Isoclines highlight amplitude resonances (blue-red colour bar).

FIGURE 8

(A) Entrainment of the modified Korenčič model to light-dark cycles as zeitgeber with a period of 24 h or drug cycles as zeitgeber with a period of 28.8 h. Entrainment to the light-dark cycles is successful and results in a limit cycle (left), but entrainment to the drug cycles results in toroidal dynamics (middle) instead. Coexisting 24 h light-dark cycles and 28.8 h drug cycles result in successful 5:6 entrainment of the circadian rhythm with “folded” limit cycles (right). (B) Example time trace of 5:6 entrainment. Zeitgeber amplitudes in all panels: r _light = 0.2 and r _+REV = 0.2.