An astonishing regularity in student learning rate

Abstract

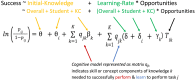
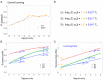
Leveraging a scientific infrastructure for exploring how students learn, we have developed cognitive and statistical models of skill acquisition and used them to understand fundamental similarities and differences across learners. Our primary question was why do some students learn faster than others? Or, do they? We model data from student performance on groups of tasks that assess the same skill component and that provide follow-up instruction on student errors. Our models estimate, for both students and skills, initial correctness and learning rate, that is, the increase in correctness after each practice opportunity. We applied our models to 1.3 million observations across 27 datasets of student interactions with online practice systems in the context of elementary to college courses in math, science, and language. Despite the availability of up-front verbal instruction, like lectures and readings, students demonstrate modest initial prepractice performance, at about 65% accuracy. Despite being in the same course, students' initial performance varies substantially from about 55% correct for those in the lower half to 75% for those in the upper half. In contrast, and much to our surprise, we found students to be astonishingly similar in estimated learning rate, typically increasing by about 0.1 log odds or 2.5% in accuracy per opportunity. These findings pose a challenge for theories of learning to explain the odd combination of large variation in student initial performance and striking regularity in student learning rate.

Keywords: deliberate practice; learning curves; learning rate; logistic regression growth modeling; educational equity.

Fig. 1.

We model success (p_ij) of student i on task j across deliberate practice opportunities (T_ik) in a logistic regression with initial-knowledge and learning-rate estimates. These estimates are each decomposed into overall, student (i), and knowledge component (k) elements. The knowledge components required by each task (j) are specified in a cognitive model matrix (q_jk).

Fig. 2.

Example learning curves from dataset 394. (A) Learning curve and model predictions average over all students and KCs. (B) Model-based learning curves for three randomly selected students showing nonlinear percentage point slopes at two different opportunities. (C) Same curves in log odds scale with intercept values (yellow) and linear slopes (blue). (D) Student i predicted success (p_i) at opportunity T as a function of intercept and slope.

Fig. 3.

Learning curves relating opportunities to practice to performance accuracy in percent correct displayed on a log odds scale. The top graphs show student learning curves indicating little variation in student learning rate (i.e., lines are mostly parallel) in contrast to large variation in initial performance. The middle graphs show knowledge component (KC) learning curves indicating that learning-rate variation is possible and measurable as these lines are not parallel. The bottom graphs demonstrate that the model can accurately identify high student learning-rate variation and low student initial performance variation when they are known to be present as determined by simulation.

Fig. 4.

Across three domains, and various grade levels, little variation is observed in student learning rate, but large differences are observed in student initial knowledge. These learning curves relate opportunities to practice to performance accuracy in percent correct displayed on a log odds scale.