Triadic influence as a proxy for compatibility in social relationships

Abstract

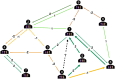
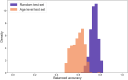
Networks of social interactions are the substrate upon which civilizations are built. Often, we create new bonds with people that we like or feel that our relationships are damaged through the intervention of third parties. Despite their importance and the huge impact that these processes have in our lives, quantitative scientific understanding of them is still in its infancy, mainly due to the difficulty of collecting large datasets of social networks including individual attributes. In this work, we present a thorough study of real social networks of 13 schools, with more than 3,000 students and 60,000 declared positive and negative relationships, including tests for personal traits of all the students. We introduce a metric-the "triadic influence"-that measures the influence of nearest neighbors in the relationships of their contacts. We use neural networks to predict the sign of the relationships in these social networks, extracting the probability that two students are friends or enemies depending on their personal attributes or the triadic influence. We alternatively use a high-dimensional embedding of the network structure to also predict the relationships. Remarkably, using the triadic influence (a simple one-dimensional metric) achieves the best accuracy, and adding the personal traits of the students does not improve the results, suggesting that the triadic influence acts as a proxy for the social compatibility of students. We postulate that the probabilities extracted from the neural networks-functions of the triadic influence and the personalities of the students-control the evolution of real social networks, opening an avenue for the quantitative study of these systems.

Keywords: machine learning; relationship prediction; social networks; triadic influence.

Fig. 1.

Diagram of a social network that includes personality traits and computation of the triadic influence. To predict the relationship from node 0 to node 1, we can use the individual features of both students (represented by the sliders within their body) and/or the triadic influence I₀₁. The directions of these relationships are marked by arrows going from the nominator to the nominee, whereas the weight/intensity is represented with colors and edge labels (dark green, close friend; green, friend; yellow, dislike; orange, enemy). Thick arrows highlight the relationships that enter the calculation of I₀₁. To compute I₀₁, we select all directed paths of length 2 from node 0 to node 1 (0 → node → 1). In this example, they are 0-5-1 and 0-6-1. The path 0-3-1 is not a directed path (the direction of the edges is 0 → 3 ← 1) and therefore is not included in the calculation of I₀₁. Thus, I₀₁ = w₀₅w₅₁ + w₀₆w₆₁ = 2 ⋅ 2 + ( − 1)⋅2 = 2.

Fig. 2.

Balanced test accuracy for different choices of information used to train the NN. Purple bars correspond to relationships where there is at least one directed path of length 2 from i to j ((A²)_ij > 0, A_ij being the adjacency matrix of the network). We train the classifier using four sets of predictors: (1) triadic influence and personal information (gender, CRT, and prosociality), (2) triadic influence alone, (3) personal information alone, and (4) just students’ prosociality. In all four cases, we trained 10 different NN with random initializations and show here the mean bAcc. Yellow bars correspond to the bAcc for relationships that have no directed paths of length 2. In this case, we use just two sets of predictors: (5) personal information and (6) students’ prosociality. These cases use 10-fold cross-validation to estimate the performance of the prediction. Error bars represent the SE of the mean in all cases.

Fig. 3.

Probabilities of being friends/enemies as a function of the triadic influence and prosociality. Panel (A) shows the probability learned by the NN as a function of the triadic influence. We performed 10 simulations that led to the accuracy shown in the (2) bar in Fig. 2. Continuous lines in panel (A) correspond to the mean, whereas the shaded area corresponds to one SE of the mean. Panel (B) shows the distribution of friends/enemies as a function of the triadic influence. Note that the probabilities in panel (A) display an asymmetry reminiscent of the distribution of the data. Panel (C) and (D) display the mean probabilities learned by the 10 NN used in Fig. 2 (4); they show the probability of having a friendly/enmity relationship as a function of the prosociality of both students, the nominator (from) and nominee (to). Both probabilities are normalized to 1.

Fig. 4.

Distribution of balanced accuracy for the 13 high schools. Each histogram is composed of a sample of N = 390 points, which are different simulations for the same treatment. The histograms are normalized so that the area under the curve is 1. The purple (dark) histogram represents treatment I where we use a random pick of edges as the test set. The orange (light) histogram represents treatment II, where we pick a specific age level from a high school as the test set. The same figure for a random forest model is included in (SI Appendix, Fig. S10).