Population dynamics of head-direction neurons during drift and reorientation
- PMID: 36949190
- PMCID: PMC10060160
- DOI: 10.1038/s41586-023-05813-2
Population dynamics of head-direction neurons during drift and reorientation
Erratum in
-
Author Correction: Population dynamics of head-direction neurons during drift and reorientation.Nature. 2023 May;617(7961):E10. doi: 10.1038/s41586-023-06126-0. Nature. 2023. PMID: 37142784 Free PMC article. No abstract available.
Abstract
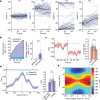
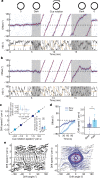
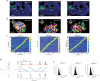
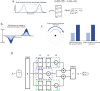
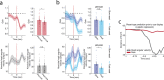
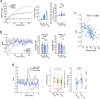
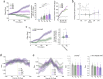
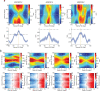
The head direction (HD) system functions as the brain's internal compass1,2, classically formalized as a one-dimensional ring attractor network3,4. In contrast to a globally consistent magnetic compass, the HD system does not have a universal reference frame. Instead, it anchors to local cues, maintaining a stable offset when cues rotate5-8 and drifting in the absence of referents5,8-10. However, questions about the mechanisms that underlie anchoring and drift remain unresolved and are best addressed at the population level. For example, the extent to which the one-dimensional description of population activity holds under conditions of reorientation and drift is unclear. Here we performed population recordings of thalamic HD cells using calcium imaging during controlled rotations of a visual landmark. Across experiments, population activity varied along a second dimension, which we refer to as network gain, especially under circumstances of cue conflict and ambiguity. Activity along this dimension predicted realignment and drift dynamics, including the speed of network realignment. In the dark, network gain maintained a 'memory trace' of the previously displayed landmark. Further experiments demonstrated that the HD network returned to its baseline orientation after brief, but not longer, exposures to a rotated cue. This experience dependence suggests that memory of previous associations between HD neurons and allocentric cues is maintained and influences the internal HD representation. Building on these results, we show that continuous rotation of a visual landmark induced rotation of the HD representation that persisted in darkness, demonstrating experience-dependent recalibration of the HD system. Finally, we propose a computational model to formalize how the neural compass flexibly adapts to changing environmental cues to maintain a reliable representation of HD. These results challenge classical one-dimensional interpretations of the HD system and provide insights into the interactions between this system and the cues to which it anchors.
© 2023. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures










References
-
- Skaggs WE, Knierim JJ, Kudrimoti HS, McNaughton BL. A model of the neural basis of the rat’s sense of direction. Adv. Neural. Inf. Process. Syst. 1995;7:173–180. - PubMed
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

