Beating the break-even point with a discrete-variable-encoded logical qubit

Abstract

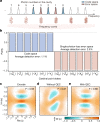
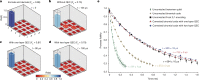
Quantum error correction (QEC) aims to protect logical qubits from noises by using the redundancy of a large Hilbert space, which allows errors to be detected and corrected in real time¹. In most QEC codes^2-8, a logical qubit is encoded in some discrete variables, for example photon numbers, so that the encoded quantum information can be unambiguously extracted after processing. Over the past decade, repetitive QEC has been demonstrated with various discrete-variable-encoded scenarios^9-17. However, extending the lifetimes of thus-encoded logical qubits beyond the best available physical qubit still remains elusive, which represents a break-even point for judging the practical usefulness of QEC. Here we demonstrate a QEC procedure in a circuit quantum electrodynamics architecture¹⁸, where the logical qubit is binomially encoded in photon-number states of a microwave cavity⁸, dispersively coupled to an auxiliary superconducting qubit. By applying a pulse featuring a tailored frequency comb to the auxiliary qubit, we can repetitively extract the error syndrome with high fidelity and perform error correction with feedback control accordingly, thereby exceeding the break-even point by about 16% lifetime enhancement. Our work illustrates the potential of hardware-efficient discrete-variable encodings for fault-tolerant quantum computation¹⁹.

Fig. 1. Schematic of the QEC procedure with the lowest-order binomially encoded logical qubit.

The auxiliary qubit is first encoded to the logical qubit in an oscillator with $\left\{∣0_{\mathrm{L}}⟩=\left(∣0⟩+∣4⟩\right)/\sqrt{2},∣1_{\mathrm{L}}⟩=∣2⟩\right\}$. Once a single-photon-jump error occurs, the logical qubit state falls out of the code space to the error space with the basis states: $\left\{∣0_{\mathrm{E}}⟩=∣3⟩,∣1_{\mathrm{E}}⟩=∣1⟩\right\}$. After repetitive error detecting and correcting, the logical qubit state is protected against single-photon-jump errors. Finally, quantum state is decoded back to the auxiliary qubit for a final state characterization. The cardinal point states in the Bloch spheres of the code and error spaces are defined as $∣+Z_{\mathrm{L}\left(\mathrm{E}\right)}⟩=∣0_{\mathrm{L}\left(\mathrm{E}\right)}⟩,∣+X_{\mathrm{L}\left(\mathrm{E}\right)}⟩=\left(∣0_{\mathrm{L}\left(\mathrm{E}\right)}⟩+∣1_{\mathrm{L}\left(\mathrm{E}\right)}⟩\right)/\sqrt{2}$ and $∣+Y_{\mathrm{L}\left(\mathrm{E}\right)}⟩=\left(∣0_{\mathrm{L}\left(\mathrm{E}\right)}⟩+i∣1_{\mathrm{L}\left(\mathrm{E}\right)}⟩\right)/\sqrt{2}$, respectively.

Fig. 2. Frequency comb control to measure the error syndrome.

a, Frequency comb control is realized by mapping the photon number parity of the logical state to the auxiliary qubit state by applying a microwave pulse with multi-frequency components to the auxiliary qubit. Two components match the auxiliary qubit frequencies when the logical qubit is in the error space and other components are chosen symmetrically for the code space to eliminate the off-resonant driving effect on the logical states. b, Bar chart of the measured photon number parities for the six cardinal point states on the Bloch spheres of the logical qubit in the code and error spaces with the frequency comb parity measurement. Solid black frames correspond to the ideal parities ± 1 for the logical states in the code and error spaces. The numbers represent the average parity detection errors in these two spaces. c, Measured Wigner function of the cavity state after encoding the logical qubit in the $∣+X_{\mathrm{L}}⟩$ state. d,e, Measured Wigner functions of the same cavity state after a waiting time of about 90 μs without (d) and with (e) a single QEC operation. The numbers in these Wigner functions represent the corresponding state fidelities. Source Data

Fig. 3. Performance of repetitive QEC operations.

a–d, Bar charts of the real parts of the process matrices for an encode and decode process (a), a waiting time of about 105 μs without QEC (b), a cycle time of about 90 μs with one-layer QEC operation (c) and a cycle time of about 180 μs with two-layer QEC operation (d). The numbers in brackets represent the process fidelities for each case. e, Process fidelity decays as a function of time for different encodings. Error bars correspond to 1 s.d. of several repeated measurements. The process fidelities for both the corrected binomial code with one-layer QEC (red triangles) and two-layer QEC (blue circles) exhibit slow decay, compared with the uncorrected Fock states $\left\{∣0⟩,∣1⟩\right\}$ encoding (black squares), which defines the break-even point in this system. The corrected binomial code with two-layer QEC offers an improvement over the break-even point by a factor of 1.2, and also surpasses the uncorrected binomial code (yellow stars) by a factor of 2.9 and the uncorrected transmon qubit (green diamonds) by a factor of 8.8. All curves are fitted using F_χ = Ae^−t/τ + 0.25 to extract the lifetimes τ of the corresponding encodings. Uncertainties on τ are obtained from the fittings. Source Data