Epidemic modeling with heterogeneity and social diffusion
- PMID: 36964799
- PMCID: PMC10039364
- DOI: 10.1007/s00285-022-01861-w
Epidemic modeling with heterogeneity and social diffusion
Abstract
We propose and analyze a family of epidemiological models that extend the classic Susceptible-Infectious-Recovered/Removed (SIR)-like framework to account for dynamic heterogeneity in infection risk. The family of models takes the form of a system of reaction-diffusion equations given populations structured by heterogeneous susceptibility to infection. These models describe the evolution of population-level macroscopic quantities S, I, R as in the classical case coupled with a microscopic variable f, giving the distribution of individual behavior in terms of exposure to contagion in the population of susceptibles. The reaction terms represent the impact of sculpting the distribution of susceptibles by the infection process. The diffusion and drift terms that appear in a Fokker-Planck type equation represent the impact of behavior change both during and in the absence of an epidemic. We first study the mathematical foundations of this system of reaction-diffusion equations and prove a number of its properties. In particular, we show that the system will converge back to the unique equilibrium distribution after an epidemic outbreak. We then derive a simpler system by seeking self-similar solutions to the reaction-diffusion equations in the case of Gaussian profiles. Notably, these self-similar solutions lead to a system of ordinary differential equations including classic SIR-like compartments and a new feature: the average risk level in the remaining susceptible population. We show that the simplified system exhibits a rich dynamical structure during epidemics, including plateaus, shoulders, rebounds and oscillations. Finally, we offer perspectives and caveats on ways that this family of models can help interpret the non-canonical dynamics of emerging infectious diseases, including COVID-19.
Keywords: COVID-19; Epidemiology; Fokker–Planck equation; Heterogeneity; Non-linear differential system; Reaction–diffusion system; SIR model; Social diffusion.
© 2023. The Author(s).
Conflict of interest statement
The authors have no conflict of interest to declare that are relevant to the content of this article.
Figures
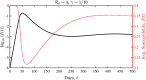
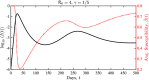

References
-
- Almeida L, Bliman PA, Nadin G, Perthame B, Vauchelet N. Final size and convergence rate for an epidemic in heterogeneous population. Math Models Methods Appl Sci. 2021;31:1021–1051. doi: 10.1142/S0218202521500251. - DOI
-
- Arnold A, Markowich P, Toscani G, Unterreiter A. On convex Sobolev inequalities and the rate of convergence to equilibrium for Fokker-Planck type equations. Commun Partial Differ Equ. 2001;26(1–2):43–100. doi: 10.1081/PDE-100002246. - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Medical

