Computational graph pangenomics: a tutorial on data structures and their applications
- PMID: 36969737
- PMCID: PMC10038355
- DOI: 10.1007/s11047-022-09882-6
Computational graph pangenomics: a tutorial on data structures and their applications
Abstract
Computational pangenomics is an emerging research field that is changing the way computer scientists are facing challenges in biological sequence analysis. In past decades, contributions from combinatorics, stringology, graph theory and data structures were essential in the development of a plethora of software tools for the analysis of the human genome. These tools allowed computational biologists to approach ambitious projects at population scale, such as the 1000 Genomes Project. A major contribution of the 1000 Genomes Project is the characterization of a broad spectrum of genetic variations in the human genome, including the discovery of novel variations in the South Asian, African and European populations-thus enhancing the catalogue of variability within the reference genome. Currently, the need to take into account the high variability in population genomes as well as the specificity of an individual genome in a personalized approach to medicine is rapidly pushing the abandonment of the traditional paradigm of using a single reference genome. A graph-based representation of multiple genomes, or a graph pangenome, is replacing the linear reference genome. This means completely rethinking well-established procedures to analyze, store, and access information from genome representations. Properly addressing these challenges is crucial to face the computational tasks of ambitious healthcare projects aiming to characterize human diversity by sequencing 1M individuals (Stark et al. 2019). This tutorial aims to introduce readers to the most recent advances in the theory of data structures for the representation of graph pangenomes. We discuss efficient representations of haplotypes and the variability of genotypes in graph pangenomes, and highlight applications in solving computational problems in human and microbial (viral) pangenomes.
Figures
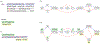


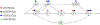
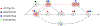



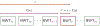
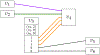
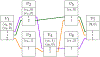
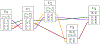



References
-
- Abouelhoda M, Kurtz S, Ohlebusch E (2004) Replacing suffix trees with enhanced suffix arrays. J Discret Algorithms 2(1):53–86. 10.1016/S1570-8667(03)00065-0 - DOI
-
- Baaijens JA, Stougie L, Schönhuth A (2020) Strain-aware assembly of genomes from mixed samples using flow variation graphs. bioRxiv:645721. 10.1101/645721 - DOI
Grants and funding
LinkOut - more resources
Full Text Sources
Miscellaneous
