Towards better understanding the stiffness of nanocomposites via parametric study of an analytical model modeling parameters and experiments
- PMID: 36974194
- PMCID: PMC10037548
- DOI: 10.1177/00219983221149122
Towards better understanding the stiffness of nanocomposites via parametric study of an analytical model modeling parameters and experiments
Abstract
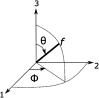
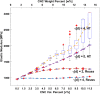
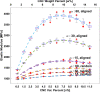
The stiffness of polymeric materials can be improved dramatically with the addition of nanoparticles. In theory, as the nanoparticle loading in the polymer increases, the nanocomposite becomes stiffer; however, experiments suggest that little or no stiffness improvement is observed beyond an optimal nanoparticle loading. The mismatch between the theoretical and experimental findings, particularly at high particle loadings, needs to be understood for the effective use of nanoparticles. In this respect, we have recently developed an analytical model to close the gap in the literature and predict elastic modulus of nanocomposites. The model is based on a three-phase Mori-Tanaka model coupled with the Monte-Carlo method, and satisfactorily captures the experimental results, even at high nanoparticle loadings. The developed model can also be used to study the effects of agglomeration in nanocomposites. In this paper, we use this model to study the effects of agglomeration and related model parameters on the stiffness of nanocomposites. In particular, the effects of particle orientation, critical distance, dispersion state and agglomerate property, and particle aspect ratio are investigated to demonstrate capabilities of the model and to observe how optimal particle loading changes with respect these parameters. The study shows that the critical distance defining agglomerates and the properties of agglomerates are the key design parameters at high particle loadings. These two parameters rule the optimal elastic modulus with respect to particle loading. The findings will allow researchers to form design curves and successfully predict the elastic moduli of nanocomposites without the exhaustive experimental undertakings.
Keywords: Monte-Carlo; Nanocomposite; modeling; mori-tanaka; parametric study.
© The Author(s) 2023.
Conflict of interest statement
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Figures





References
-
- Fornes TD, Paul DR. Modeling properties of nylon 6/clay nanocomposites using composite theories. Polymer (Guildf) 2003; 44: 4993–5013. DOI: 10.1016/S0032-3861(03)00471-3 - DOI
-
- Sheng N, Boyce MC, Parks DM, et al. Multiscale micromechanical modeling of polymer/clay nanocomposites and the effective clay particle. Polymer (Guildf) 2004; 45: 487–506. DOI: 10.1016/j.polymer.2003.10.100 - DOI
-
- Vera-Agullo J, Glória-Pereira A, Varela-Rizo H, et al. Comparative study of the dispersion and functional properties of multiwall carbon nanotubes and helical-ribbon carbon nanofibers in polyester nanocomposites. Compos Sci Technol 2009; 69: 1521–1532. DOI: 10.1016/j.compscitech.2008.11.032 - DOI
-
- Shi D-L, Feng X-Q, Huang YY, et al. The effect of nanotube waviness and agglomeration on the elastic property of carbon nanotube-reinforced composites. J Eng Mater Technol Trans ASME 2004; 126: 250–257. DOI: 10.1115/1.1751182 - DOI
-
- Corrêa AC, Teodoro KBR, Simão JA, et al. Cellulose nanocrystals from curaua fibers and poly[ethylene-co-(vinyl acetate)] nanocomposites: effect of drying process of CNCs on thermal and mechanical properties. Polym Compos 2020; 41: 1736–1748. DOI: 10.1002/pc.25493 - DOI
LinkOut - more resources
Full Text Sources
Miscellaneous
