Towards better understanding the stiffness of nanocomposites via parametric study of an analytical model modeling parameters and experiments

Abstract

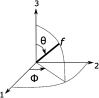
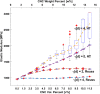
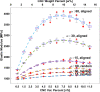
The stiffness of polymeric materials can be improved dramatically with the addition of nanoparticles. In theory, as the nanoparticle loading in the polymer increases, the nanocomposite becomes stiffer; however, experiments suggest that little or no stiffness improvement is observed beyond an optimal nanoparticle loading. The mismatch between the theoretical and experimental findings, particularly at high particle loadings, needs to be understood for the effective use of nanoparticles. In this respect, we have recently developed an analytical model to close the gap in the literature and predict elastic modulus of nanocomposites. The model is based on a three-phase Mori-Tanaka model coupled with the Monte-Carlo method, and satisfactorily captures the experimental results, even at high nanoparticle loadings. The developed model can also be used to study the effects of agglomeration in nanocomposites. In this paper, we use this model to study the effects of agglomeration and related model parameters on the stiffness of nanocomposites. In particular, the effects of particle orientation, critical distance, dispersion state and agglomerate property, and particle aspect ratio are investigated to demonstrate capabilities of the model and to observe how optimal particle loading changes with respect these parameters. The study shows that the critical distance defining agglomerates and the properties of agglomerates are the key design parameters at high particle loadings. These two parameters rule the optimal elastic modulus with respect to particle loading. The findings will allow researchers to form design curves and successfully predict the elastic moduli of nanocomposites without the exhaustive experimental undertakings.

Keywords: Monte-Carlo; Nanocomposite; modeling; mori-tanaka; parametric study.

Figure 1.

Schematics of the homogenization approach.

Figure 2.

Schematics of an agglomerate for better understanding of a center-to-center distance.

Figure 3.

The definitions of $\theta ,Ф,$ and $fiber\hspace{0.17em}\mathit{f}$ in a Cartesian coordinate system.

Figure 4.

Elastic modulus predictions of cellulose nanocrystals with polyamide 6 (CNC-PA6) composite as a function of CNC loading for (a) aligned and (b) randomly oriented particles at various $\gamma \left[d\right]$ values.

Figure 5.

The effect of $\gamma \left[d\right]$ and agglomerate’s property on the elastic modulus of randomly particle nanocomposites based on the Reuss and Halpin-Tsai (HT) used for agglomeration.

Figure 6.

Predictions of the longitudinal elastic modulus of CNC-PA6 composites as a function of CNC concentrations for various orientation and aspect ratio ($\alpha$) of the particles.

Figure 7.

Predictions of elastic modulus of nanocomposites as functions of $\gamma \left[d\right]$ and $\mu \left[d\right]$ at 1.0 (a), 2.5 (b), 5.0 (c), 7.5 (d), 10.0 (e) and 15.0 (f) w% of CNC and corresponding experimental findings from shown with black spheres.

Figure 8.

Predictions of elastic modulus of nanocomposites with respect to CNC concentration and experimental findings adapted from.