Pattern dynamics and stochasticity of the brain rhythms
- PMID: 36976768
- PMCID: PMC10083604
- DOI: 10.1073/pnas.2218245120
Pattern dynamics and stochasticity of the brain rhythms
Abstract
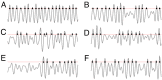
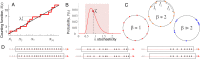
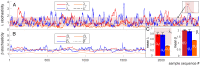
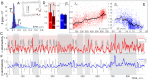
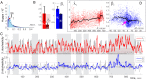
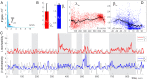
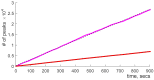
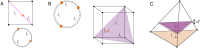
Our current understanding of brain rhythms is based on quantifying their instantaneous or time-averaged characteristics. What remains unexplored is the actual structure of the waves-their shapes and patterns over finite timescales. Here, we study brain wave patterning in different physiological contexts using two independent approaches: The first is based on quantifying stochasticity relative to the underlying mean behavior, and the second assesses "orderliness" of the waves' features. The corresponding measures capture the waves' characteristics and abnormal behaviors, such as atypical periodicity or excessive clustering, and demonstrate coupling between the patterns' dynamics and the animal's location, speed, and acceleration. Specifically, we studied patterns of θ, γ, and ripple waves recorded in mice hippocampi and observed speed-modulated changes of the wave's cadence, an antiphase relationship between orderliness and acceleration, as well as spatial selectiveness of patterns. Taken together, our results offer a complementary-mesoscale-perspective on brain wave structure, dynamics, and functionality.
Keywords: hippocampus; learning and memory; patterning; waveforms.
Conflict of interest statement
The authors declare no competing interest.
Figures

Similar articles
-
Different theta frameworks coexist in the rat hippocampus and are coordinated during memory-guided and novelty tasks.Elife. 2020 Jul 20;9:e57313. doi: 10.7554/eLife.57313. Elife. 2020. PMID: 32687054 Free PMC article.
-
Rhythms of the hippocampal network.Nat Rev Neurosci. 2016 Apr;17(4):239-49. doi: 10.1038/nrn.2016.21. Epub 2016 Mar 10. Nat Rev Neurosci. 2016. PMID: 26961163 Free PMC article. Review.
-
Speed controls the amplitude and timing of the hippocampal gamma rhythm.PLoS One. 2011;6(6):e21408. doi: 10.1371/journal.pone.0021408. Epub 2011 Jun 24. PLoS One. 2011. PMID: 21731735 Free PMC article.
-
[Sensory processing could be temporally organized by ultradian brain rhythms].Rev Neurol. 2005 Feb 1-15;40(3):166-72. Rev Neurol. 2005. PMID: 15750903 Review. Spanish.
-
Oscillations and hippocampal-prefrontal synchrony.Curr Opin Neurobiol. 2011 Jun;21(3):467-74. doi: 10.1016/j.conb.2011.04.006. Epub 2011 May 14. Curr Opin Neurobiol. 2011. PMID: 21571522 Free PMC article. Review.
Cited by
-
Altered patterning of neural activity in a neuropathology.Sci Rep. 2025 Jul 16;15(1):25881. doi: 10.1038/s41598-025-08538-6. Sci Rep. 2025. PMID: 40670446 Free PMC article.
-
Theta Oscillons in Behaving Rats.J Neurosci. 2025 May 14;45(20):e0164242025. doi: 10.1523/JNEUROSCI.0164-24.2025. J Neurosci. 2025. PMID: 40169263
-
Altered patterning of neural activity in a tauopathy mouse model.bioRxiv [Preprint]. 2024 Mar 27:2024.03.23.586417. doi: 10.1101/2024.03.23.586417. bioRxiv. 2024. Update in: Sci Rep. 2025 Jul 16;15(1):25881. doi: 10.1038/s41598-025-08538-6. PMID: 38585991 Free PMC article. Updated. Preprint.
-
Theta oscillons in behaving rats.ArXiv [Preprint]. 2024 Apr 22:arXiv:2404.13851v1. ArXiv. 2024. Update in: J Neurosci. 2025 May 14;45(20):e0164242025. doi: 10.1523/JNEUROSCI.0164-24.2025. PMID: 38711435 Free PMC article. Updated. Preprint.
-
Theta oscillons in behaving rats.bioRxiv [Preprint]. 2024 Apr 25:2024.04.21.590487. doi: 10.1101/2024.04.21.590487. bioRxiv. 2024. Update in: J Neurosci. 2025 May 14;45(20):e0164242025. doi: 10.1523/JNEUROSCI.0164-24.2025. PMID: 38712230 Free PMC article. Updated. Preprint.
References
-
- Buzsáki G., Rhythms in the Brain (Oxford University Press, New York, 2011).
-
- Skaggs W., McNaughton B., Wilson M., Barnes C., Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6, 149–172 (1996). - PubMed
-
- Bench K., et al. , Coherent theta oscillations and reorganization of spike timing in the hippocampal- prefrontal network upon learning. Neuron 66, 921–936 (2010). - PubMed
-
- Nikoli D., Fries P., Singer W., Gamma oscillations: Precise temporal coordination without a metronome. Trends Cogn. Sci. 17, 54–55 (2013). - PubMed
-
- Colgin L., et al. , Frequency of gamma oscillations routes flow of information in the hippocampus. Nature 462, 353–357 (2009). - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

