Analysis of Von Kármán Swirling Flows Due to a Porous Rotating Disk Electrode

Abstract

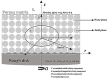
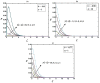
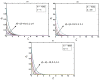
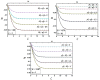
The study of Von Kármán swirling flow is a subject of active interest due to its applications in a wide range of fields, including biofuel manufacturing, rotating heat exchangers, rotating disc reactors, liquid metal pumping engines, food processing, electric power generating systems, designs of multi-pore distributors, and many others. This paper focusses on investigating Von Kármán swirling flows of viscous incompressible fluid due to a rotating disk electrode. The model is based on a system of four coupled second-order non-linear differential equations. The purpose of the present communication is to derive analytical expressions of velocity components by solving the non-linear equations using the homotopy analysis method. Combined effects of the slip λ and porosity γ parameters are studied in detail. If either parameter is increased, all velocity components are reduced, as both have the same effect on the mean velocity profiles. The porosity parameter γ increases the moment coefficient at the disk surface, which monotonically decreases with the slip parameter λ. The analytical results are also compared with numerical solutions, which are in satisfactory agreement. Furthermore, the effects of porosity and slip parameters on velocity profiles are discussed.

Keywords: homotopy analysis method; mathematical modeling; non-linear differential equations; rotating disk electrodes.

Figure 1

The coordinate system of the Von Kármán flow in a porous medium with its boundary conditions.

Figure 2

(a–c) Plots of the normalized radial velocity component $F$ versus normalized distance from the disk $\zeta$ using Equation (13) for various values of parameters. Solid lines represent Equation (13) and dotted lines represent the numerical solutions [44].

Figure 3

(a–c) Plots of the normalized tangential velocity component $G$ versus normalized distance from the disk $\zeta$ using Equation (14) for various values of parameters. Solid lines represent Equation (14) and dotted lines represent the numerical solutions [44].

Figure 4

(a–c) Plots of the normalized axial velocity component $H$ versus normalized distance from the disk $\zeta$ using Equation (15) for various values of parameters. Solid lines represent Equation (15) and dotted lines represent the numerical solutions [44].

Figure 5

The sensitivity of parameters: percentage changes in normalized velocity components $F, G \mathrm{and} H$ when $\lambda =1, \eta =1, \gamma =1 at \zeta =1$.