Autopolyploidy, Allopolyploidy, and Phylogenetic Networks with Horizontal Arcs

Abstract

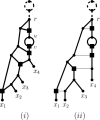
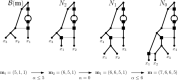
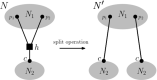
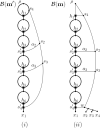
Polyploidization is an evolutionary process by which a species acquires multiple copies of its complete set of chromosomes. The reticulate nature of the signal left behind by it means that phylogenetic networks offer themselves as a framework to reconstruct the evolutionary past of species affected by it. The main strategy for doing this is to first construct a so-called multiple-labelled tree and to then somehow derive such a network from it. The following question therefore arises: How much can be said about that past if such a tree is not readily available? By viewing a polyploid dataset as a certain vector which we call a ploidy (level) profile, we show that among other results, there always exists a phylogenetic network in the form of a beaded phylogenetic tree with additional arcs that realizes a given ploidy profile. Intriguingly, the two end vertices of almost all of these additional arcs can be interpreted as having co-existed in time thereby adding biological realism to our network, a feature that is, in general, not enjoyed by phylogenetic networks. In addition, we show that our network may be viewed as a generator of ploidy profile space, a novel concept similar to phylogenetic tree space that we introduce to be able to compare phylogenetic networks that realize one and the same ploidy profile. We illustrate our findings in terms of a publicly available Viola dataset.

Keywords: Phylogenetic network; Ploidy profile; Ploidy profile space; Polyploid phylogenetics.

Fig. 1

(i) One of potentially many phylogenetic networks that realize the ploidy levels 14, 12, 12, 10 of a set $X=\{x_1,x_2,x_3,x_4\}$ of taxa where 14 is the ploidy level of $x_1$, the ploidy level of $x_2$ and $x_3$ is 12, respectively, and the ploidy level of $x_4$ is 10. To improve clarity of exposition, we always assume that unless indicated otherwise, arcs are directed away from the root (which is always at the top). (ii) The network in (i) represented in such a way that every reticulation vertex (indicated throughout the paper by a square and defined below) has precisely one incoming horizontal arc implying that the end vertices of such an arc represent ancestral species that have existed at the same point in time. In both (i) and (ii), the phylogenetic network resulting from deleting the dashed bead and its dashed outgoing arc realizes the ploidy profile $\mathbf{m}=(7,6,6,5)$

Fig. 2

When reading from left to right, the construction of $N(\mathbf{m})$ obtained from the traceback through the simplification sequence $\sigma (\mathbf{m})$ for the ploidy profile $\mathbf{m}=(7,6,6,5)$ on $\{x_1,\dots ,x_4\}$. The ploidy profiles that make up $\sigma (\mathbf{m})$ are given at the bottom. The terminal element ${\mathbf{m}}_{\mathbf{t}}$ of $\sigma (\mathbf{m})$ is the ploidy profile (5, 1, 1), and the phylogenetic network $\mathcal{B}(\mathbf{m})$ on the left is a core network for $\mathbf{m}$. The cases that apply in each step of the traceback are indicated below the arrows between the four ploidy profiles that make up $\sigma (\mathbf{m})$. The thin horizontal arcs relate to the example illustrating Theorem 1

Fig. 3

An illustration of the split operation applied to the reticulation vertex h with parents $p_1$ and $p_2$ and child c. $N_1$ and $N_2$ indicate parts of the multiple-labelled networks N and $N^{\prime }$ that are of no relevance to the discussion

Fig. 4

(i) Core network $\mathcal{B}({\mathbf{m}}^{\prime })$ for the strictly simple ploidy profile ${\mathbf{m}}^{\prime }=(77)$ on $X=\{x_1\}$. (ii) The core network $\mathcal{B}(\mathbf{m})$ for the simple ploidy profile $\mathbf{m}=(77,1,1,1)$ on $\{x_1,x_2,x_3,x_4\}$ obtained from $\mathcal{B}({\mathbf{m}}^{\prime })$. Alternative core networks for $\mathbf{m}$ can be obtained from $\mathcal{B}({\mathbf{m}}^{\prime })$ by subdividing non-bold arcs and attaching the remaining elements of X as phylogenetic trees on subsets of X or individually (ensuring that the arc $(s_3,s_4^{\prime })$ is subdivided at a least once as otherwise the resulting phylogenetic network does not admit a HGT-consistent labelling because Property (P3) is violated)

Fig. 5

(i) Realization $\mathcal{B}(\mathbf{m})$ of the practical ploidy profile $\mathbf{m}=(12,1,1)$ on $X=\{x_1,x_2,x_3\}$. (ii) A core network for $\mathbf{m}$ that is not of the form $\mathcal{B}(\mathbf{m})$

Fig. 6

Realization $N^{\prime }$ of the ploidy profile ${\mathbf{m}}^{\prime }=(40,24,8,4,2,1)$ in terms of a phylogenetic network with horizontal arcs

Fig. 7

A complete cherry modification sequence for the core network $\mathcal{B}(\mathbf{m})$ of $\mathbf{m}=(7,6,6,5)$. The applied cherry modifications operations are indicated above the arrows between the networks

Fig. 8

A weak cherry modification sequence for the realization $N(\mathbf{m})$, depicted on the left, of the ploidy profile $\mathbf{m}=(6,3)$ on $\{x_1,x_2\}$

Fig. 9

(i) A phylogenetic network on $X=\{$rubellium, viola, V.verecunda, V.blande, V.repens, V.933palustris, V.721palustris, V.macloskeyi, V.langsdorff, V.tracheliffolia, V.grahamii, V.glabella$\}$ adapted from Marcussen et al. (2012). To improve clarity, we include the ploidy level of each reticulation vertex. Apart from rubellium and viola which are denoted ru and vi, respectively, leaves are labelled by the first two characters of their name (omitting “V.”). (ii) The realization $N(\mathbf{m})$ of the ploidy profile $\mathbf{m}$ induced by the network in (i). Contrary to the network in (i), $N(\mathbf{m})$ is orchard. In each case, the graph obtained by removing the non-bold arcs is a base tree for $N(\mathbf{m})$. For ease of readability, the labels of the non-leaf vertices represent the number of directed paths from the root to that vertex in each of (i) and (ii)