Quantitative assessment can stabilize indirect reciprocity under imperfect information
- PMID: 37045828
- PMCID: PMC10097696
- DOI: 10.1038/s41467-023-37817-x
Quantitative assessment can stabilize indirect reciprocity under imperfect information
Abstract
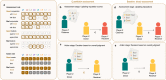
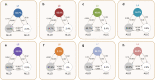
The field of indirect reciprocity investigates how social norms can foster cooperation when individuals continuously monitor and assess each other's social interactions. By adhering to certain social norms, cooperating individuals can improve their reputation and, in turn, receive benefits from others. Eight social norms, known as the "leading eight," have been shown to effectively promote the evolution of cooperation as long as information is public and reliable. These norms categorize group members as either 'good' or 'bad'. In this study, we examine a scenario where individuals instead assign nuanced reputation scores to each other, and only cooperate with those whose reputation exceeds a certain threshold. We find both analytically and through simulations that such quantitative assessments are error-correcting, thus facilitating cooperation in situations where information is private and unreliable. Moreover, our results identify four specific norms that are robust to such conditions, and may be relevant for helping to sustain cooperation in natural populations.
© 2023. The Author(s).
Conflict of interest statement
The authors declare no competing interests.
Figures







Similar articles
-
Indirect reciprocity with stochastic and dual reputation updates.PLoS Comput Biol. 2023 Jul 20;19(7):e1011271. doi: 10.1371/journal.pcbi.1011271. eCollection 2023 Jul. PLoS Comput Biol. 2023. PMID: 37471286 Free PMC article.
-
Indirect reciprocity under incomplete observation.PLoS Comput Biol. 2011 Jul;7(7):e1002113. doi: 10.1371/journal.pcbi.1002113. Epub 2011 Jul 28. PLoS Comput Biol. 2011. PMID: 21829335 Free PMC article.
-
Social norm complexity and past reputations in the evolution of cooperation.Nature. 2018 Mar 7;555(7695):242-245. doi: 10.1038/nature25763. Nature. 2018. PMID: 29516999
-
The complexity of human cooperation under indirect reciprocity.Philos Trans R Soc Lond B Biol Sci. 2021 Nov 22;376(1838):20200291. doi: 10.1098/rstb.2020.0291. Epub 2021 Oct 4. Philos Trans R Soc Lond B Biol Sci. 2021. PMID: 34601904 Free PMC article. Review.
-
A pull versus push framework for reputation.Trends Cogn Sci. 2023 Sep;27(9):852-866. doi: 10.1016/j.tics.2023.06.005. Epub 2023 Jul 17. Trends Cogn Sci. 2023. PMID: 37468335 Review.
Cited by
-
The evolution of private reputations in information-abundant landscapes.Nature. 2024 Oct;634(8035):883-889. doi: 10.1038/s41586-024-07977-x. Epub 2024 Sep 25. Nature. 2024. PMID: 39322674
-
Picking strategies in games of cooperation.Proc Natl Acad Sci U S A. 2025 Jun 24;122(25):e2319925121. doi: 10.1073/pnas.2319925121. Epub 2025 Jun 16. Proc Natl Acad Sci U S A. 2025. PMID: 40523167 Free PMC article.
-
A mechanistic model of gossip, reputations, and cooperation.Proc Natl Acad Sci U S A. 2024 May 14;121(20):e2400689121. doi: 10.1073/pnas.2400689121. Epub 2024 May 8. Proc Natl Acad Sci U S A. 2024. PMID: 38717858 Free PMC article.
-
Imitation dynamics on networks with incomplete information.Nat Commun. 2023 Nov 17;14(1):7453. doi: 10.1038/s41467-023-43048-x. Nat Commun. 2023. PMID: 37978181 Free PMC article.
-
Indirect reciprocity in the public goods game with collective reputations.J R Soc Interface. 2025 Apr;22(225):20240827. doi: 10.1098/rsif.2024.0827. Epub 2025 Apr 2. J R Soc Interface. 2025. PMID: 40170565 Free PMC article.
References
-
- Alexander, R. The Biology of Moral Systems (Aldine de Gruyter, 1987).
-
- Bolton GE, Katok E, Ockenfels A. Cooperation among strangers with limited information about reputation. J. Public Econ. 2005;89:1457–68. doi: 10.1016/j.jpubeco.2004.03.008. - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources
Research Materials

