Signatures of Electric Field and Layer Separation Effects on the Spin-Valley Physics of MoSe2/WSe2 Heterobilayers: From Energy Bands to Dipolar Excitons

Abstract

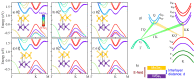
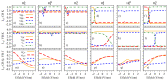
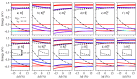
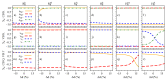
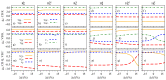
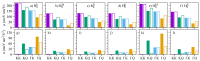
Multilayered van der Waals heterostructures based on transition metal dichalcogenides are suitable platforms on which to study interlayer (dipolar) excitons, in which electrons and holes are localized in different layers. Interestingly, these excitonic complexes exhibit pronounced valley Zeeman signatures, but how their spin-valley physics can be further altered due to external parameters-such as electric field and interlayer separation-remains largely unexplored. Here, we perform a systematic analysis of the spin-valley physics in MoSe2/WSe2 heterobilayers under the influence of an external electric field and changes of the interlayer separation. In particular, we analyze the spin (Sz) and orbital (Lz) degrees of freedom, and the symmetry properties of the relevant band edges (at K, Q, and Γ points) of high-symmetry stackings at 0° (R-type) and 60° (H-type) angles-the important building blocks present in moiré or atomically reconstructed structures. We reveal distinct hybridization signatures on the spin and the orbital degrees of freedom of low-energy bands, due to the wave function mixing between the layers, which are stacking-dependent, and can be further modified by electric field and interlayer distance variation. We find that H-type stackings favor large changes in the g-factors as a function of the electric field, e.g., from -5 to 3 in the valence bands of the Hhh stacking, because of the opposite orientation of Sz and Lz of the individual monolayers. For the low-energy dipolar excitons (direct and indirect in k-space), we quantify the electric dipole moments and polarizabilities, reflecting the layer delocalization of the constituent bands. Furthermore, our results show that direct dipolar excitons carry a robust valley Zeeman effect nearly independent of the electric field, but tunable by the interlayer distance, which can be rendered experimentally accessible via applied external pressure. For the momentum-indirect dipolar excitons, our symmetry analysis indicates that phonon-mediated optical processes can easily take place. In particular, for the indirect excitons with conduction bands at the Q point for H-type stackings, we find marked variations of the valley Zeeman (∼4) as a function of the electric field, which notably stands out from the other dipolar exciton species. Our analysis suggests that stronger signatures of the coupled spin-valley physics are favored in H-type stackings, which can be experimentally investigated in samples with twist angle close to 60°. In summary, our study provides fundamental microscopic insights into the spin-valley physics of van der Waals heterostructures, which are relevant to understanding the valley Zeeman splitting of dipolar excitonic complexes, and also intralayer excitons.

Keywords: TMDC; spin-valley; valley Zeeman; van der Waals heterostructure.

Figure 1

(a–f) calculated band structures, with the color-coded layer decomposition of the wave function for (a) R${}_{\mathrm{h}}^{\mathrm{h}}$, (b) R${}_{\mathrm{h}}^{\mathrm{M}}$, (c) R${}_{\mathrm{h}}^{\mathrm{X}}$, (d) H${}_{\mathrm{h}}^{\mathrm{h}}$, (e) H${}_{\mathrm{h}}^{\mathrm{M}}$, and (f) H${}_{\mathrm{h}}^{\mathrm{X}}$ stackings; the insets show the side-view of the crystal structures (solid lines connect the hollow position of the bottom layer to the atomic registry of the top layer); (g) relevant low-energy bands and possible interlayer exciton transitions originating from the top valence bands at the $\mathsf{\Gamma }$ (v${}_{\mathsf{\Gamma }}$) and K points (v${}_{\mathrm{W}}$); the transitions involving the time-reversal partners (−K and −Q points) are not shown, for simplicity; (h) schematic representation of the applied external electric field and the interlayer distance.

Figure 2

Spin-resolved band structures for the (a) R${}_{\mathrm{h}}^{\mathrm{h}}$, (b) R${}_{\mathrm{h}}^{\mathrm{M}}$, (c) R${}_{\mathrm{h}}^{\mathrm{X}}$, (d) H${}_{\mathrm{h}}^{\mathrm{h}}$, (e) H${}_{\mathrm{h}}^{\mathrm{M}}$, and (f) H${}_{\mathrm{h}}^{\mathrm{X}}$ stackings.

Figure 3

Energy dependence with respect to the electric field of the relevant low-energy bands (see Figure 1g) for all considered stackings: the top row, panels (a–f), indicates the color-coded layer decomposition of the K point bands (same color code as in Figure 1a–f); the bottom row, panels (g–l), indicates the color-coded spin decomposition of the K point bands (same color code as in Figure 2a–f); the insets in panels (g–l) show the energy difference between ${\mathrm{c}}_{\mathrm{Q}+}$ and ${\mathrm{c}}_{\mathrm{Q}-}$ bands, emphasizing an anti-crossing at larger electric fields.

Figure 4

Spin degree of freedom, $S_z$, of the low-energy bands as a function of the applied electric field for the studied stackings R${}_{\mathrm{h}}^{\mathrm{h}}$ (a,g,m), R${}_{\mathrm{h}}^{\mathrm{M}}$ (b,h,n), R${}_{\mathrm{h}}^{\mathrm{X}}$ (c,i,o), H${}_{\mathrm{h}}^{\mathrm{h}}$ (d,j,p), H${}_{\mathrm{h}}^{\mathrm{M}}$ (e,k,q), and H${}_{\mathrm{h}}^{\mathrm{X}}$ (f,l,r).

Figure 5

Same as Figure 4 but for the orbital degree freedom, $L_z$.

Figure 6

Same as Figure 4 and Figure 5 but for the band g-factor, $g_z=L_z+S_z$.

Figure 7

Same as Figure 3 but as a function of the interlayer distance variation.

Figure 8

Same as Figure 4 but as a function of the interlayer distance variation.

Figure 9

Same as Figure 5 but as a function of the interlayer distance variation.

Figure 10

Same as Figure 6 but as a function of the interlayer distance variation.

Figure 11

Calculated values of the electric dipole moments for (a) R${}_{\mathrm{h}}^{\mathrm{h}}$, (b) R${}_{\mathrm{h}}^{\mathrm{M}}$, (c) R${}_{\mathrm{h}}^{\mathrm{X}}$, (d) H${}_{\mathrm{h}}^{\mathrm{h}}$, (e) H${}_{\mathrm{h}}^{\mathrm{M}}$, and (f) H${}_{\mathrm{h}}^{\mathrm{X}}$ stackings. Calculated values of the polarizabilities for (g) R${}_{\mathrm{h}}^{\mathrm{h}}$, (h) R${}_{\mathrm{h}}^{\mathrm{M}}$, (i) R${}_{\mathrm{h}}^{\mathrm{X}}$, (j) H${}_{\mathrm{h}}^{\mathrm{h}}$, (k) H${}_{\mathrm{h}}^{\mathrm{M}}$, and (l) H${}_{\mathrm{h}}^{\mathrm{X}}$ stackings. The x-axis indicates the type of dipolar excitons (see Figure 1g. The values originating from ${\mathrm{c}}_{\mathrm{M}/\mathrm{Q}-}$ (${\mathrm{c}}_{\mathrm{M}/\mathrm{Q}+}$) are shown with colored (open) boxes.

Figure 12

Absolute value of the dipole matrix element for interlayer transitions at the K point as a function of the electric field for (a) R${}_{\mathrm{h}}^{\mathrm{h}}$, (b) R${}_{\mathrm{h}}^{\mathrm{M}}$, (c) R${}_{\mathrm{h}}^{\mathrm{X}}$, (d) H${}_{\mathrm{h}}^{\mathrm{h}}$, (e) H${}_{\mathrm{h}}^{\mathrm{M}}$, and (f) H${}_{\mathrm{h}}^{\mathrm{X}}$ stackings.

Figure 13

Calculated ratio ${\tau }_{\mathrm{rad}}\left(F_z\right)/{\tau }_{\mathrm{rad}}\left(0\right)$ as a function of the electric field for (a) R${}_{\mathrm{h}}^{\mathrm{h}}$, (b) R${}_{\mathrm{h}}^{\mathrm{M}}$, (c) R${}_{\mathrm{h}}^{\mathrm{X}}$, (d) H${}_{\mathrm{h}}^{\mathrm{h}}$, (e) H${}_{\mathrm{h}}^{\mathrm{M}}$, and (f) H${}_{\mathrm{h}}^{\mathrm{X}}$ stackings. We use $E_0=1.35$ eV for all cases, and the calculated values of $\mu$ given in Figure 11. The contribution of $\alpha$ is neglected, as they nearly vanish for KK dipolar excitons.

Figure 14

Dipolar exciton g-factors as a function of the electric field for the R- and H-type systems studied for the cases (a–f) $\left|g\left(c\right)-g\left({\mathrm{v}}_{\mathrm{W}}\right)\right|$, (g–l) $\left|g\left(c\right)+g\left({\mathrm{v}}_{\mathrm{W}}\right)\right|$, (m–r) $\left|g\left(c\right)-g\left({\mathrm{v}}_{\mathsf{\Gamma }}\right)\right|$ and (s–v,x,y) $\left|g\left(c\right)+g\left({\mathrm{v}}_{\mathsf{\Gamma }}\right)\right|$.

Figure 15

Same as Figure 12 but as a function o the interlayer distance.

Figure 16

Same as Figure 14 but as a function of the interlayer distance.