Inferring the mode and strength of ongoing selection
- PMID: 37055196
- PMCID: PMC10234300
- DOI: 10.1101/gr.276386.121
Inferring the mode and strength of ongoing selection
Abstract
Genome sequence data are no longer scarce. The UK Biobank alone comprises 200,000 individual genomes, with more on the way, leading the field of human genetics toward sequencing entire populations. Within the next decades, other model organisms will follow suit, especially domesticated species such as crops and livestock. Having sequences from most individuals in a population will present new challenges for using these data to improve health and agriculture in the pursuit of a sustainable future. Existing population genetic methods are designed to model hundreds of randomly sampled sequences but are not optimized for extracting the information contained in the larger and richer data sets that are beginning to emerge, with thousands of closely related individuals. Here we develop a new method called trio-based inference of dominance and selection (TIDES) that uses data from tens of thousands of family trios to make inferences about natural selection acting in a single generation. TIDES further improves on the state of the art by making no assumptions regarding demography, linkage, or dominance. We discuss how our method paves the way for studying natural selection from new angles.
© 2023 Barroso and Lohmueller; Published by Cold Spring Harbor Laboratory Press.
Figures
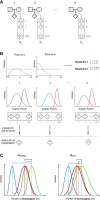
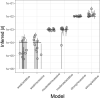





References
-
- Barroso GV, Dutheil JY. 2021. Mutation rate variation shapes genome-wide diversity in Drosophila melanogaster. bioRxiv 10.1101/2021.09.16.460667 - DOI
