This is a preprint.
Fluorescence Microscopy: a statistics-optics perspective
- PMID: 37064525
- PMCID: PMC10104198
Fluorescence Microscopy: a statistics-optics perspective
Abstract
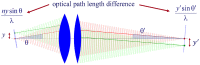
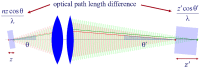
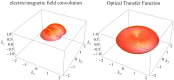
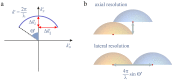
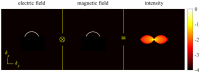
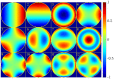
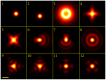
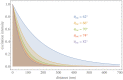
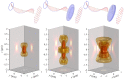
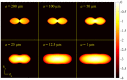
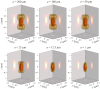
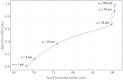
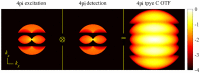
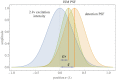
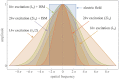
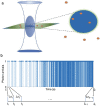
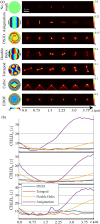
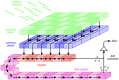
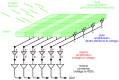
Fundamental properties of light unavoidably impose features on images collected using fluorescence microscopes. Modeling these features is ever more important in quantitatively interpreting microscopy images collected at scales on par or smaller than light's wavelength. Here we review the optics responsible for generating fluorescent images, fluorophore properties, microscopy modalities leveraging properties of both light and fluorophores, in addition to the necessarily probabilistic modeling tools imposed by the stochastic nature of light and measurement.
Figures












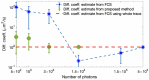

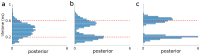
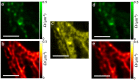
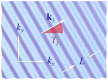





References
-
- Darrigol O., A history of optics from Greek antiquity to the nineteenth century (Oxford University Press, 2012).
-
- Thibodeau P., Ancient optics: Theories and problems of vision, A Companion to Science, Technology, and Medicine in Ancient Greece and Rome, 2 Volume Set, 130 (2016).
-
- Wang J. and Wang C., Optics in China, in Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures, edited by Selin H. (Springer Netherlands, Dordrecht, 2008) pp. 1790–1792.
-
- Smith A. M. et al., Ptolemy’s theory of visual perception: an English translation of the optics, Vol. 82 (American Philosophical Society, 1996).
-
- Nasr S. H. and De Santillana G., Science and civilization in Islam, Vol. 16 (Harvard University Press; Cambridge, MA, 1968).
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
