Free energy and inference in living systems

Abstract

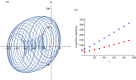
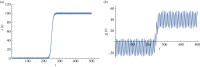
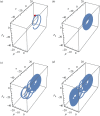
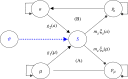
Organisms are non-equilibrium, stationary systems self-organized via spontaneous symmetry breaking and undergoing metabolic cycles with broken detailed balance in the environment. The thermodynamic free-energy (FE) principle describes an organism's homeostasis as the regulation of biochemical work constrained by the physical FE cost. By contrast, recent research in neuroscience and theoretical biology explains a higher organism's homeostasis and allostasis as Bayesian inference facilitated by the informational FE. As an integrated approach to living systems, this study presents an FE minimization theory overarching the essential features of both the thermodynamic and neuroscientific FE principles. Our results reveal that the perception and action of animals result from active inference entailed by FE minimization in the brain, and the brain operates as a Schrödinger's machine conducting the neural mechanics of minimizing sensory uncertainty. A parsimonious model suggests that the Bayesian brain develops the optimal trajectories in neural manifolds and induces a dynamic bifurcation between neural attractors in the process of active inference.

Keywords: Bayesian brain; Schrödinger’s machine; free-energy principle; homeostasis and allostasis; living system; neural attractor.

Figure 1.

Spontaneous attractor: for illustrational purposes, we depict the attractor in the 3D state space spanned by $(\mathrm{Re}[\mu ],\mathrm{Re}[a],\mathrm{Re}[p_{\mu }])$ with instantaneous other variables; the attractor centre, ${\Psi }_c$, is positioned at (−10, 10, −20). The full attractor evolves in the hyper space spanned by the eight components of complex vector, $\Psi$; in our model, there are the four types of neuronal units $(\mu ,a,p_{\mu },p_a)$ in a single cortical-column, each of which is allowed to be a complex variable. (Data are in arbitrary units.)

Figure 2.

Latent dynamics under static sensory inputs: (a) attractor developed from a resting state, $\Psi (0)$, and driven by the static input s = 100, using the same parameter values as in figure 1; the initial state was chosen from the spontaneous states in figure 1, and for illustrational purposes, the attractor is depicted in the two-dimensional state space spanned by $(\mathrm{Re}[{\Psi }_2],\mathrm{Re}[{\Psi }_4])$. (b) Cognitive intensity, $|{\Psi }_c{|}^2$, versus sensory input, s. The filled squares are the results from the neural inertial masses $(m_z,m_w,m_{\eta })=(10,1,10)$ and open circles are the results from $(m_z,m_w,m_{\eta })=(1,1,1)$; the numerical values for the other generative parameters are the same as those used in figure 1. (Data are in arbitrary units.)

Figure 3.

Active dynamics under time-dependent sensory inputs: (a) salient feature of streaming perturbation at the receptor state, s(t); we assume a sigmoid shape for the temporal dependence with the saturated value s_∞ = 100, stiffness k = 0.2, and mid-time t_m = 250. (b) Motor inference of the sensory signals; the BM was integrated using the same parameter values as in figure 2a for the generative parameters and neural masses. (All curves are in arbitrary units.)

Figure 4.

Attractor dynamics inferring the non-stationary sensory influx depicted in figure 3a: (a) t = 5, (b) t = 100, (c) t = 260 and (d) t = 500. The trajectory, $\Psi (t)$, results from the direct numerical integration of the BM described by equations (4.18)–(4.21); the initial state, $\Psi (0)=(-16.9,21.1,-13.3)$, was selected from the spontaneous attractor given in figure 1. For numerical purposes, the attractor evolution is depicted in the three-dimensional state space spanned by $(\mathrm{Re}[\mu ],\mathrm{Re}[a],\mathrm{Re}[p_{\mu }])$. The numerical values adopted for all parameters are the same as those in figure 3. (Data are in arbitrary units.)

Figure 5.

Schematic of the neural circuitry exhibiting the double closed-loop architecture of perception and action, which emerges from the Bayesian mechanics prescribed by equations (4.18)–(4.21).