High-dimensional principal component analysis with heterogeneous missingness

Abstract

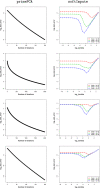
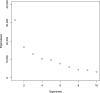
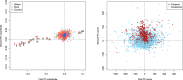
We study the problem of high-dimensional Principal Component Analysis (PCA) with missing observations. In a simple, homogeneous observation model, we show that an existing observed-proportion weighted (OPW) estimator of the leading principal components can (nearly) attain the minimax optimal rate of convergence, which exhibits an interesting phase transition. However, deeper investigation reveals that, particularly in more realistic settings where the observation probabilities are heterogeneous, the empirical performance of the OPW estimator can be unsatisfactory; moreover, in the noiseless case, it fails to provide exact recovery of the principal components. Our main contribution, then, is to introduce a new method, which we call primePCA, that is designed to cope with situations where observations may be missing in a heterogeneous manner. Starting from the OPW estimator, primePCA iteratively projects the observed entries of the data matrix onto the column space of our current estimate to impute the missing entries, and then updates our estimate by computing the leading right singular space of the imputed data matrix. We prove that the error of primePCA converges to zero at a geometric rate in the noiseless case, and when the signal strength is not too small. An important feature of our theoretical guarantees is that they depend on average, as opposed to worst-case, properties of the missingness mechanism. Our numerical studies on both simulated and real data reveal that primePCA exhibits very encouraging performance across a wide range of scenarios, including settings where the data are not Missing Completely At Random.

Keywords: heterogeneous missingness; high‐dimensional statistics; iterative projections; missing data; principal component analysis.

FIGURE 1

An illustration of the two steps of a single iteration of the primePCA algorithm with $d=3$ and $K=1$. Black dots represent fully observed data points, while vertical dotted lines that emanate from them give an indication of their $x_3$ coordinate values, as well as their projections onto the $x_1$‐$x_2$ plane. The $x_1$ coordinate of the orange data point and the $x_2$ coordinate of the blue data point are unobserved, so the true observations lie on the respective solid lines through those points (which are parallel to the relevant axes). Starting from an input estimate of ${\mathbf{V}}_K$ (left), given by the black arrow, we impute the missing coordinates as the closest points on the coloured lines to ${\mathbf{V}}_K$ (middle), and then obtain an updated estimate of ${\mathbf{V}}_K$ as the leading right singular vector of the imputed data matrix (right, with the old estimate in grey). [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 2

Estimates of $𝔼L({\widehat{\mathbf{V}}}_K^{\text{prime}},{\mathbf{V}}_K)$ for various choices of ${\sigma }_{\ast }$ under (H1) in the noiseless setting of Section 4.1 (left) and (H2) in the noisy setting of Section 4.2 with $\nu =20$ (right)

FIGURE 3

Logarithms of the average Frobenius norm $\sin \mathrm{\Theta }$ error of primePCA and softImpute under various heterogeneity levels of missingness in absence of noise. The four rows of plots above, from the top to bottom, correspond to (H1), (H2), (H3) and (H4). [Colour figure can be viewed at wileyonlinelibrary.com]

FIGURE 4

Leading eigenvalues of ${\widehat{\mathbf{\sum }}}_{\mathbf{y}}$

FIGURE 5

Plots of the first two principal components ${\widehat{\mathbf{V}}}_2^{\text{prime}}$ (left) and the associated scores ${\{{\widehat{\mathbf{u}}}_i\}}_{i=1}^n$ (right) [Colour figure can be viewed at wileyonlinelibrary.com]