Representation of the inferred relationships in a map-like space

Abstract

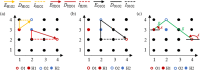
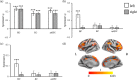
A cognitive map is an internal representation of the external world that guides flexible behavior in a complex environment. Cognitive map theory assumes that relationships between entities can be organized using Euclidean-based coordinates. Previous studies revealed that cognitive map theory can also be generalized to inferences about abstract spaces, such as social spaces. However, it is still unclear whether humans can construct a cognitive map by combining relational knowledge between discrete entities with multiple abstract dimensions in nonsocial spaces. Here we asked subjects to learn to navigate a novel object space defined by two feature dimensions, price and abstraction. The subjects first learned the rank relationships between objects in each feature dimension and then completed a transitive inferences task. We recorded brain activity using functional magnetic resonance imaging (fMRI) while they performed the transitive inference task. By analyzing the behavioral data, we found that the Euclidean distance between objects had a significant effect on response time (RT). The longer the one-dimensional rank distance and two-dimensional (2D) Euclidean distance between objects the shorter the RT. The task-fMRI data were analyzed using both univariate analysis and representational similarity analysis. We found that the hippocampus, entorhinal cortex, and medial orbitofrontal cortex were able to represent the Euclidean distance between objects in 2D space. Our findings suggest that relationship inferences between discrete objects can be made in a 2D nonsocial space and that the neural basis of this inference is related to cognitive maps.

Keywords: decision making; entorhinal cortex; hippocampus; learning; medial orbitofrontal cortex; transitive inference.

FIGURE 1

Object hierarchy and experimental procedures. (a) Object hierarchy. The subjects needed to learn the rank of 16 artificial objects separately in two dimensions: price (yellow square) and abstraction (gray square). These objects were randomly divided into two groups (group 1 and group 2), each containing 8 objects of different colors (4 red objects) to ensure that the object color was balanced between the two different groups. (b) Experimental procedures. The subjects attended the behavioral training before the fMRI scanning. They learned the rank relationships of the within‐group objects in each of two dimensions and completed the test on days 1 and 2, separately. On day 3, they learned the rank relationships of between‐group objects (hub learning). Afterward, they were invited to attend the MRI scanning on the same day. During the fMRI scanning, they were required to infer the relative ranks between novel paired objects. After the scanning, the subjects needed to complete the placement task. (c) An example trial of the fMRI experiment. The subjects made inferences about the relative ranks of a novel paired objects (O1 and O2) in the task‐relevant dimension (shown by the cue color) without any feedback. A color judgement task (O3) followed at the end of the trial.

FIGURE 2

The hub objects and nonhub objects in the two dimensions. (a) Four objects as hub in each dimension. (b) Twelve objects served as nonhubs in each dimension.

FIGURE 3

Different distance and vector angle measures in the 2D object space. (a) The subjects could use different hub objects (H1 or H2) to infer the rank difference between the novel paired objects. They could use either inference from O1 to a hub object (H1) that has a connection with O2 (D _H1O2, E _H1O2; yellow) or inference from O2 to a hub object (H2) that has a connection with O1 (D _H2O1, E _H2O1; red). (b) The subjects might not use the hub objects but might instead compute the rank difference between O1 and O2 in the given dimension or their Euclidean distance to infer the rank relationship between the novel paired objects (D _O1O2, E _O1O2; blue). (c) Measures of Euclidean distance and vector angle in a 2D space defined by the price and abstraction dimensions. The cosine vector angle represents the normalized function of abstraction modulated by price. The circles denote different object positions on the map; D and I denote the rank distance between objects on the task‐relevant dimension and the task‐irrelevant dimension, respectively; E and A denote the Euclidean distance and cosine vector angle between objects, respectively.

FIGURE 4

The masks for fMRI data analyses and the results obtained from behavioral analysis. (a) Brain masks of the hippocampus (HC), medial orbitofrontal cortex (mOFC), and entorhinal cortex (EC). These masks (regions of interest, ROIs) were defined according to the Brainnetome atlas (Fan et al., 2016) and were used for the univariate analysis and the representation similarity analysis. (b) RT explained by different distance measures in LMM1. The results showed that the Euclidean distance and rank distance between H2 and O1 in the task‐relevant dimension explained RT variance. Error bars indicate the standard error.

FIGURE 5

Model RDMs based on different distance measures in the object space. (a) Euclidean distance between the paired objects in the 2D object space. (b) The 1D rank distance between the paired objects in the price dimension. (c) The 1D rank distance between the paired objects in the abstraction dimension.

FIGURE 6

ROI‐based RSA. Spearman's ρ shows to what extent the model RDM of the Euclidean distance and the rank distance can explain the pattern dissimilarity between voxels in each of the ROIs. (a) The bilateral HC, EC, and mOFC represented the Euclidean distance between objects in the 2D space. (b) 1D rank distance on the price dimension. (c) same to (b) but for the abstraction dimension. We found that the left HC, rather than the other ROIs, represents the 1D rank distance between objects. ***p < .001. (d) The brain regions obtained from the searchlight RSA. Abbreviations: HC, hippocampus; EC, entorhinal cortex; mOFC, medial orbitofrontal cortex; L (R), left (right) hemisphere.