Correction of errors in estimates of T1ρ at low spin-lock amplitudes in the presence of B0 and B1 inhomogeneities

Abstract

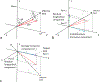
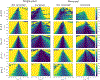
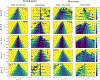
Relaxation rates R_1ρ in the rotating frame measured by spin-lock methods at very low locking amplitudes (≤ 100 Hz) are sensitive to the effects of water diffusion in intrinsic gradients and may provide information on tissue microvasculature, but accurate estimates are challenging in the presence of B₀ and B₁ inhomogeneities. Although composite pulse preparations have been developed to compensate for nonuniform fields, the transverse magnetization comprises different components and the spin-lock signals measured do not decay exponentially as a function of locking interval at low locking amplitudes. For example, during a typical preparation sequence, some of the magnetization in the transverse plane is nutated to the Z-axis and later tipped back, and so does not experience R_1ρ relaxation. As a result, if the spin-lock signals are fit to a monoexponential decay with locking interval, there are residual errors in quantitative estimates of relaxation rates R_1ρ and their dispersion with weak locking fields. We developed an approximate theoretical analysis to model the behaviors of the different components of the magnetization, which provides a means to correct these errors. The performance of this correction approach was evaluated both through numerical simulations and on human brain images at 3 T, and compared with a previous correction method using matrix multiplication. Our correction approach has better performance than the previous method at low locking amplitudes. Through careful shimming, the correction approach can be applied in studies using low spin-lock amplitudes to assess the contribution of diffusion to R_1ρ dispersion and to derive estimates of microvascular sizes and spacings. The results of imaging eight healthy subjects suggest that R_1ρ dispersion in human brain at low locking fields arises from diffusion among inhomogeneities that generate intrinsic gradients on a scale of capillaries (~7.4 ± 0.5 μm).

Keywords: R1ρ fitting error; diffusion; low power; microvasculature; spin-lock; susceptibility gradients; vessel size.

FIG. 1.

Diagram of spin-lock sequences with the conventional pulse (a) and the composite pulse preparation cluster (b).

FIG. 2.

(a) Schematic diagram to show the nutation of water magnetization (solid red arrow) about the effective field (dashed black arrow) in the first half of the composite pulse preparation cluster. Dashed red arrow shows the magnetization after the first ${90}_{\mathrm{x}}$ excitation pulse but before the spin-lock preparation cluster. (b) shows the instantaneous transverse component (light blue arrow) and the two residual longitudinal components: part 1 (purple arrow) and part 2 (green arrow) during the first half of the composite pulse preparation cluster. (c) shows the average transverse component (light blue arrow) and the part 1 of the residual longitudinal component (purple arrow) that tipped back into the transverse plane after the second half of the composite pulse preparation cluster. The black dotted arrows show the motion trajectory of the magnetization as well as their transverse and longitudinal components. Note that the part 1 of the residual longitudinal component in (b) and (c) are not necessarily to be equal.

FIG. 3.

Single-pool model simulated spin-lock signal vs. $\mathrm{\tau }$ using the conventional rectangular (a, c) and the composite pulse (b, d) preparation cluster, respectively, at ${\mathrm{\omega }}_1$ of 0 Hz (blue), 20 Hz (red), and 500 Hz (green). (a, b) show simulations with ${\mathrm{B}}_0$ shift $(\mathrm{\Delta }{\mathrm{\omega }}_{\text{off}}=10\mathrm{H}\mathrm{z})$, but no ${\mathrm{B}}_1$ shift $(\mathrm{\beta }=1)$. (c, d) show simulations with no ${\mathrm{B}}_0$ shift $(\mathrm{\Delta }{\mathrm{\omega }}_{\text{off}}=0\mathrm{H}\mathrm{z})$, but with ${\mathrm{B}}_1$ shift $(\mathrm{\beta }=0.9)$. Simulated spin-lock signals with no shifts in either ${\mathrm{B}}_0$ $(\mathrm{\Delta }{\mathrm{\omega }}_{\text{off}}=0\mathrm{H}\mathrm{z})$ or ${\mathrm{B}}_1$ $(\mathrm{\beta }=1)$ with ${\mathrm{\omega }}_1$ of 50 Hz (light blue) were also plotted in each subfigure as true spin-lock signals for comparison. The green and the light blue lines in (a) overlap. The blue, green, and light blue lines in (b) overlap. The red, green, and light blue lines in (d) overlap.

FIG. 4.

Spin-lock signals using the composite pulse preparation clusters vs. $\mathrm{\tau }$ for the single-pool (a, c, e) and two-pool (b, d, f) models through numerical simulations (blue lines), calculated using our approximate formula Eq. (4) and Eq. (5) (red lines), as well as calculated using the rotation matrix multiplication approach (green lines) with ${\mathrm{\omega }}_1$ of 20 Hz under ${\mathrm{B}}_0$ shifts ($\mathrm{\Delta }{\mathrm{\omega }}_{\text{off}}=0$ (dashed lines) and 10 Hz (solid lines), $\mathrm{\beta }=1),{\mathrm{B}}_1$ shifts ($\mathrm{\beta }=1$ (dashed lines) and 0.9 (solid lines), $\mathrm{\Delta }{\mathrm{\omega }}_{\text{off}}=0\mathrm{H}\mathrm{z}$), and both ${\mathrm{B}}_0$ and ${\mathrm{B}}_1$ shifts ($\mathrm{\Delta }{\mathrm{\omega }}_{\text{off}}=0$ (dashed lines) and 10 Hz (solid lines), $\mathrm{\beta }=0.9$). In all sub-figures, all dashed lines overlap. Corresponding residuals with the same colors (subtraction of the simulated data and the calculated data) are shown under each sub-figures.

FIG. 5.

Monte Carlo simulation of the ${\mathrm{R}}_{1\mathrm{\rho }}$ dispersions under ${\mathrm{B}}_0$ shift (a, b), ${\mathrm{B}}_1$ shift (c, d), and both ${\mathrm{B}}_0$ and ${\mathrm{B}}_1$ shift (e, f) without correction (blue line), corrected by approximate formula (red line), and corrected by matrix multiplication (green line) using the single-pool (a, c, e) and the two-pool (b, d, f) model. Simulations with no ${\mathrm{B}}_0$ and ${\mathrm{B}}_1$ shifts (black line) were also plotted for comparison. ${\mathrm{R}}_{1\mathrm{\rho }}$ values with ${\mathrm{\omega }}_1=0\mathrm{H}\mathrm{z}$ and 10 Hz corrected by the matrix multiplication are not shown due to the large fitting uncertainty. The SNR of the added noise is 125. Simulations were performed with ${\mathrm{\omega }}_1$ of 0, 10, 20, 30, 40, 50, 70, 80, 90, 100, 200, 300, 400, and 500Hz.

FIG. 6.

Relative change of the fitted ${\mathrm{R}}_{1\mathrm{\rho }}$ values under ${\mathrm{B}}_0$ and ${\mathrm{B}}_1$ shifts with/without correction using our approach from the true ${\mathrm{R}}_{1\mathrm{\rho }}$ values without ${\mathrm{B}}_0$ and ${\mathrm{B}}_1$ shifts $(│\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{d}{\mathrm{R}}_{1\mathrm{\rho }}–\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}{\mathrm{R}}_{1\mathrm{\rho }}│/\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}{\mathrm{R}}_{1\mathrm{\rho }})$ in the single-pool and two-pool model simulations.

FIG. 7.

Relative change of the fitted ${\mathrm{R}}_{1\mathrm{\rho }}$ values under ${\mathrm{B}}_0$ and ${\mathrm{B}}_1$ shifts with/without correction using the rotation matrix multiplication from the true ${\mathrm{R}}_{1\mathrm{\rho }}$ values without ${\mathrm{B}}_0$ and ${\mathrm{B}}_1$ shifts $(│\mathrm{f}\mathrm{i}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{d}{\mathrm{R}}_{1\mathrm{\rho }}–\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}{\mathrm{R}}_{1\mathrm{\rho }}│/\mathrm{t}\mathrm{r}\mathrm{u}\mathrm{e}{\mathrm{R}}_{1\mathrm{\rho }})$ in the single-pool and two-pool model simulations.

FIG. 8

Simulated ${\mathrm{R}}_{1\mathrm{\rho }}$ dispersions obtained with a certain true ${\mathrm{B}}_0$ shift (i.e. $\mathrm{\Delta }{\mathrm{\omega }}_{\text{off}}=10\mathrm{H}\mathrm{z},\mathrm{\beta }=1$) (a, b) and true ${\mathrm{B}}_1$ shift (i.e. $\mathrm{\Delta }{\mathrm{\omega }}_{\text{off}}=0\mathrm{H}\mathrm{z},\mathrm{\beta }=0.9$) (c, d), but using a series of measured ${\mathrm{B}}_0$ shifts or ${\mathrm{B}}_1$ shifts which deviate from the true ${\mathrm{B}}_0$ and ${\mathrm{B}}_1$ shifts, respectively, for correction using our approximate formula.

FIG. 9

Maps of ${\mathrm{T}}_2$ weighted anatomy (a), ${\mathrm{R}}_{1\mathrm{\rho }}$ with ${\mathrm{\omega }}_1$ of 100 Hz (b), ${\mathrm{B}}_0$ shift (c), ${\mathrm{B}}_1$ shift (d), $\mathrm{R}$ without correction, with correction using the matrix multiplication, and with correction using our approximate formula (f, g, h), as well as $\mathrm{g}$ without correction, with correction using the matrix multiplication, and with correction using our approximate formula (i, j, k) from human subject #1. (e) shows the averaged ${\mathrm{R}}_{1\mathrm{\rho }}$ dispersions without correction, with correction using the matrix multiplication, and with correction using our approximate formula from the whole brain.