Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 Apr 18;13(1):6287.
doi: 10.1038/s41598-023-30795-6.

Marangoni convection in dissipative flow of nanofluid through porous space

Ikram Ullah  1 , Mohammad Mahtab Alam  2 , Muhammad Irfan Shah  3 , Wajaree Weera  4
Affiliations

Marangoni convection in dissipative flow of nanofluid through porous space

Ikram Ullah et al. Sci Rep. .

Retraction in

Abstract

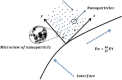
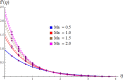
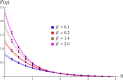
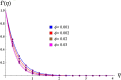
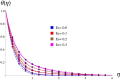
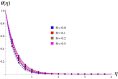
In various machinery engines, the engine oil is utilized as a lubricant. Heat transportation rate and to saving the energy dissipated due to higher temperature are the basic goals of all thermal systems. Thus, current work is mainly focused to develop a model for the Marangoni flow of nanofluids (NFs) with viscous dissipation. The considered NFs are made of nanoparticles (NPs) i.e. [Formula: see text] and base fluid (BF) as Engine Oil (EO). Darcy Forchheimer (DF) law which leads to porous medium is implemented in the model to investigate the variations of NF velocity and temperature. The governing flow expressions are simplified through similarity variables. The obtained expressions are solved numerically via an effective technique known as the NDSolve algorithm. The consequences of pertinent variables on temperature, velocity and Nusselt number are designed through tables and graphs. The obtained results reveal that velocity rises for higher Marangoni number, Darcy Forchheimer (DF) parameter whereas it shows decaying behavior against nanoparticles volume fraction.

PubMed Disclaimer

Conflict of interest statement

The authors declare no competing interests.

Figures

Figure 1
Figure 1
The modeled flow problem geometric configuration.
Figure 2
Figure 2
Behavior of velocity f′η against Ma = 0.5,1.0,1.5, 2.0.
Figure 3
Figure 3
Behavior of velocity f′η against β = 0.1, 0.2,1.4, 2.0.
Figure 4
Figure 4
Behavior of velocity f′η against Fr = 0.0, 0.5,1.0,1.5.
Figure 5
Figure 5
Behavior of velocity f′η against ϕ = 0.001, 0.002, 0.02, 0.03.
Figure 6
Figure 6
Behavior of temperature θη against Ec = 0.0, 0.1, 0.3, 0.4.
Figure 7
Figure 7
Behavior of temperature θη against Fr = 0.0, 0.1, 0.2, 0.5.
Figure 8
Figure 8
Behavior of temperature θη against ϕ = 0.001, 0.002, 0.02, 0.03.
See this image and copyright information in PMC

References

    1. Ullah I, Hayat T, Alsaedi A, Fardoun HM. Numerical treatment of melting heat transfer and entropy generation in stagnation point flow of hybrid nanomaterials (SWCNT-MWCNT/engine oil) Mod. Phys. Lett. B. 2021;35(06):2150102. doi: 10.1142/S0217984921501025. - DOI
    1. Susrutha B, Ram S, Tyagi AK. Effects of gold nanoparticles on rheology of nanofluids containing poly (vinylidene fluoride) molecules. J. Nanofluids. 2012;1(2):120–127. doi: 10.1166/jon.2012.1023. - DOI
    1. Phule AD, Ram S, Tyagi AK. Anchoring silver with poly (vinylidene fluoride) molecules in model flocculates and its effects on rheology in stable nanofluids. J. Nanofluids. 2013;2(4):249–260. doi: 10.1166/jon.2013.1067. - DOI
    1. Singh GP, Ram S. Magnetic Nanofluids: Synthesis and Applications” in “Nanofluids, Research, Development and Applications. Nova Publisher; 2013.
    1. Choi SUS, Singer DA, Wang HP. Developments and applications of non-Newtonian flows. ASME Fed. 1995;66:99–105.

Publication types