Native qudit entanglement in a trapped ion quantum processor

Abstract

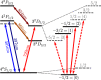
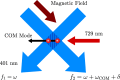
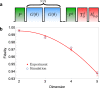
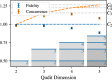
Quantum information carriers, just like most physical systems, naturally occupy high-dimensional Hilbert spaces. Instead of restricting them to a two-level subspace, these high-dimensional (qudit) quantum systems are emerging as a powerful resource for the next generation of quantum processors. Yet harnessing the potential of these systems requires efficient ways of generating the desired interaction between them. Here, we experimentally demonstrate an implementation of a native two-qudit entangling gate up to dimension 5 in a trapped-ion system. This is achieved by generalizing a recently proposed light-shift gate mechanism to generate genuine qudit entanglement in a single application of the gate. The gate seamlessly adapts to the local dimension of the system with a calibration overhead that is independent of the dimension.

Fig. 1. Level scheme of the ⁴⁰Ca⁺ ion.

Encoding quantum information in the sub-levels of the S_1/2 and D_5/2 manifold allows us to increase the size of the computational Hilbert space. Coherent operations between the sub-levels can be performed using 729 nm laser light, while 401 nm light is used to generate the light shift for the state-dependent force.

Fig. 2. Experimental setup.

Two beams with λ = 401 nm and frequencies f₁,  f₂ with a relative detuning of ω_COM + δ are intersected at a 90^∘ angle to drive the state-dependent force. A 729 nm laser along the axial trap direction is used to implement local operations.

Fig. 3. Application of the gate on two qutrits.

a Phase evolution of the two-qutrit state components relative to the $\mid 00⟩$ ground state during the application of the LS gate pulses. States $\mid 01⟩$ and $\mid 10⟩$ are shown in orange, $\mid 02⟩$ and $\mid 20⟩$ in blue, and $\mid 21⟩$ and $\mid 12⟩$ in green. The equal electronic states $\mid 00⟩,\mid 11⟩,\mid 22⟩$ in purple do not acquire any relative phases. b Corresponding pulse scheme to implement the composite qudit light-shift gate operator G(θ) for a qutrit (d = 3). Light-shift gate pulses U_LS(t_g) are interlaced with cyclic permutation gates X₃.

Fig. 4. Fidelity decay measured using multiple gates.

a Schematic of the measurement sequence. Two ions initialized in $∣00⟩$ are rotated into an equal superposition of all states by applying the operator P with the 729 nm laser. After applying the gate operator G(θ) a variable number of times n a reversed preparation pulse P^† is applied. The populations of the resulting state are measured by a set of transfer pulses $T_0^j$, which are resonant π pulses between $∣0⟩\leftrightarrow ∣j⟩$ to transfer the state $∣j⟩$ to the S_1/2 manifold, allowing us to distinguish the qudit states. An analysis pulse $A_{0,\varphi }^j$ consisting of a resonant π/2 pulse between $∣0⟩\leftrightarrow ∣j⟩$ with variable phase ϕ is used to measure the coherence between the $∣0⟩$ and $∣j⟩$ levels. Combined with the transfer pulses, all pairwise coherences can be measured. b A plot of qudit gate fidelity as a function of dimension. The average gate fidelities, shown as red circles, are extracted from fits to the fidelity decay when applying multiple gates G(θ) between P and P^†. The error bars correspond to 1 standard deviation in the fit parameters. A quadratic curve has been fitted to the data to highlight the empirically observed scaling of the fidelity with dimension. The simulated fidelities from a detailed noise model are shown as blue diamonds, see supplementary note 2 for details.

Fig. 5. Generation of genuine qudit entanglement.

The measured state fidelity for d = 2, 3, 4, 5 is shown as blue data points and the corresponding concurrence as orange squares. The ideal values for maximally entangled states (the experimental target states) are shown as dashed (dotted) lines. The gray shaded bars represent the lower bound on the fidelity (blue data points) for certifying maximal Schmidt number entanglement, while the gray horizontal lines indicate the concurrence C_d for a maximally entangled state in dimension d. Error bars correspond to one standard deviation of experimental shot noise.