High curvature promotes fusion of lipid membranes: Predictions from continuum elastic theory
- PMID: 37077047
- PMCID: PMC10209146
- DOI: 10.1016/j.bpj.2023.04.018
High curvature promotes fusion of lipid membranes: Predictions from continuum elastic theory
Abstract
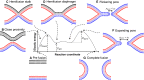
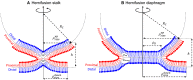
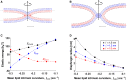
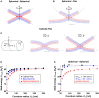
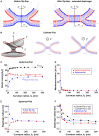
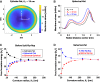
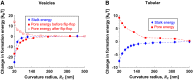
The fusion of lipid membranes progresses through a series of hemifusion intermediates with two significant energy barriers related to the formation of stalk and fusion pore, respectively. These energy barriers determine the speed and success rate of many critical biological processes, including the fusion of highly curved membranes, for example synaptic vesicles and enveloped viruses. Here we use continuum elastic theory of lipid monolayers to determine the relationship between membrane shape and energy barriers to fusion. We find that the stalk formation energy decreases with curvature by up to 31 kBT in a 20-nm-radius vesicle compared with planar membranes and by up to 8 kBT in the fusion of highly curved, long, tubular membranes. In contrast, the fusion pore formation energy barrier shows a more complicated behavior. Immediately after stalk expansion to the hemifusion diaphragm, the fusion pore formation energy barrier is low (15-25 kBT) due to lipid stretching in the distal monolayers and increased tension in highly curved vesicles. Therefore, the opening of the fusion pore is faster. However, these stresses relax over time due to lipid flip-flop from the proximal monolayer, resulting in a larger hemifusion diaphragm and a higher fusion pore formation energy barrier, up to 35 kBT. Therefore, if the fusion pore fails to open before significant lipid flip-flop takes place, the reaction proceeds to an extended hemifusion diaphragm state, which is a dead-end configuration in the fusion process and can be used to prevent viral infections. In contrast, in the fusion of long tubular compartments, the surface tension does not accumulate due to the formation of the diaphragm, and the energy barrier for pore expansion increases with curvature by up to 11 kBT. This suggests that inhibition of polymorphic virus infection could particularly target this feature of the second barrier.
Copyright © 2023 Biophysical Society. Published by Elsevier Inc. All rights reserved.
Conflict of interest statement
Declaration of interests The authors declare no competing interests.
Figures
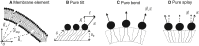
Similar articles
-
Calculating Transition Energy Barriers and Characterizing Activation States for Steps of Fusion.Biophys J. 2016 Mar 8;110(5):1110-24. doi: 10.1016/j.bpj.2016.01.013. Biophys J. 2016. PMID: 26958888 Free PMC article.
-
Calculation of free energy barriers to the fusion of small vesicles.Biophys J. 2008 Mar 1;94(5):1699-706. doi: 10.1529/biophysj.107.119511. Epub 2007 Nov 16. Biophys J. 2008. PMID: 18024495 Free PMC article.
-
Membrane Tension Inhibits Lipid Mixing by Increasing the Hemifusion Stalk Energy.ACS Nano. 2023 Oct 10;17(19):18942-18951. doi: 10.1021/acsnano.3c04293. Epub 2023 Sep 5. ACS Nano. 2023. PMID: 37669531 Free PMC article.
-
The mechanisms of lipid-protein rearrangements during viral infection.Bioelectrochemistry. 2004 Jun;63(1-2):129-36. doi: 10.1016/j.bioelechem.2003.10.016. Bioelectrochemistry. 2004. PMID: 15110263 Review.
-
Membrane fusion: the process and its energy suppliers.Cell Mol Life Sci. 2002 Sep;59(9):1478-90. doi: 10.1007/s00018-002-8523-6. Cell Mol Life Sci. 2002. PMID: 12440770 Free PMC article. Review.
Cited by
-
A microfluidic platform for the controlled synthesis of architecturally complex liquid crystalline nanoparticles.Sci Rep. 2023 Aug 4;13(1):12684. doi: 10.1038/s41598-023-39205-3. Sci Rep. 2023. PMID: 37542147 Free PMC article.
-
Inverse Bicontinuous and Discontinuous Phases of Lipids, and Membrane Curvature.Cells. 2025 May 14;14(10):716. doi: 10.3390/cells14100716. Cells. 2025. PMID: 40422219 Free PMC article. Review.
-
Hemifusomes and Interacting Proteolipid Nanodroplets Mediate Multi-Vesicular Body Formation.Res Sq [Preprint]. 2024 Oct 21:rs.3.rs-5200876. doi: 10.21203/rs.3.rs-5200876/v1. Res Sq. 2024. Update in: Nat Commun. 2025 May 17;16(1):4609. doi: 10.1038/s41467-025-59887-9. PMID: 39502775 Free PMC article. Updated. Preprint.
-
How Cell-Penetrating Peptides Behave Differently from Pore-Forming Peptides: Structure and Stability of Induced Transmembrane Pores.J Am Chem Soc. 2023 Dec 6;145(48):26095-26105. doi: 10.1021/jacs.3c08014. Epub 2023 Nov 21. J Am Chem Soc. 2023. PMID: 37989570 Free PMC article.
-
Sphingolipids containing very long-chain fatty acids regulate Ypt7 function during the tethering stage of vacuole fusion.J Biol Chem. 2024 Nov;300(11):107808. doi: 10.1016/j.jbc.2024.107808. Epub 2024 Sep 21. J Biol Chem. 2024. PMID: 39307308 Free PMC article.
References
-
- Jahn R., Grubmüller H. Membrane fusion. Curr. Opin. Cell Biol. 2002;14:488–495. - PubMed
Publication types
MeSH terms
Substances
LinkOut - more resources
Full Text Sources

