TMS-evoked responses are driven by recurrent large-scale network dynamics
- PMID: 37083491
- PMCID: PMC10121222
- DOI: 10.7554/eLife.83232
TMS-evoked responses are driven by recurrent large-scale network dynamics
Abstract
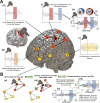
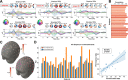
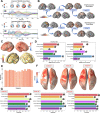
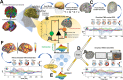
A compelling way to disentangle the complexity of the brain is to measure the effects of spatially and temporally synchronized systematic perturbations. In humans, this can be non-invasively achieved by combining transcranial magnetic stimulation (TMS) and electroencephalography (EEG). Spatiotemporally complex and long-lasting TMS-EEG evoked potential (TEP) waveforms are believed to result from recurrent, re-entrant activity that propagates broadly across multiple cortical and subcortical regions, dispersing from and later re-converging on, the primary stimulation site. However, if we loosely understand the TEP of a TMS-stimulated region as the impulse response function of a noisy underdamped harmonic oscillator, then multiple later activity components (waveform peaks) should be expected even for an isolated network node in the complete absence of recurrent inputs. Thus emerges a critically important question for basic and clinical research on human brain dynamics: what parts of the TEP are due to purely local dynamics, what parts are due to reverberant, re-entrant network activity, and how can we distinguish between the two? To disentangle this, we used source-localized TMS-EEG analyses and whole-brain connectome-based computational modelling. Results indicated that recurrent network feedback begins to drive TEP responses from 100 ms post-stimulation, with earlier TEP components being attributable to local reverberatory activity within the stimulated region. Subject-specific estimation of neurophysiological parameters additionally indicated an important role for inhibitory GABAergic neural populations in scaling cortical excitability levels, as reflected in TEP waveform characteristics. The novel discoveries and new software technologies introduced here should be of broad utility in basic and clinical neuroscience research.
Keywords: computational model; connectome; electroencephalography; human; neural mass model; neuroscience; recurrence; transcranial magnetic stimulation.
© 2023, Momi, Wang et al.
Conflict of interest statement
DM, ZW, JG No competing interests declared
Figures




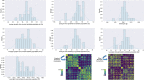
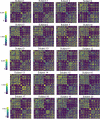





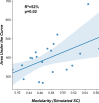
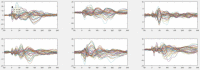















Update of
- doi: 10.1101/2022.06.09.494069
Similar articles
-
A structured ICA-based process for removing auditory evoked potentials.Sci Rep. 2022 Jan 26;12(1):1391. doi: 10.1038/s41598-022-05397-3. Sci Rep. 2022. PMID: 35082350 Free PMC article.
-
Pinging the brain with transcranial magnetic stimulation reveals cortical reactivity in time and space.Brain Stimul. 2021 Mar-Apr;14(2):304-315. doi: 10.1016/j.brs.2021.01.018. Epub 2021 Jan 28. Brain Stimul. 2021. PMID: 33516859 Free PMC article. Clinical Trial.
-
Investigating the Origin of TMS-evoked Brain Potentials Using Topographic Analysis.Brain Topogr. 2022 Nov;35(5-6):583-598. doi: 10.1007/s10548-022-00917-w. Epub 2022 Oct 26. Brain Topogr. 2022. PMID: 36289133
-
Identification and verification of a 'true' TMS evoked potential in TMS-EEG.J Neurosci Methods. 2022 Aug 1;378:109651. doi: 10.1016/j.jneumeth.2022.109651. Epub 2022 Jun 14. J Neurosci Methods. 2022. PMID: 35714721 Review.
-
The contribution of TMS-EEG coregistration in the exploration of the human cortical connectome.Neurosci Biobehav Rev. 2015 Feb;49:114-24. doi: 10.1016/j.neubiorev.2014.12.014. Epub 2014 Dec 22. Neurosci Biobehav Rev. 2015. PMID: 25541459 Review.
Cited by
-
The alterations of repetitive transcranial magnetic stimulation on the energy landscape of resting-state networks differ across the human cortex.Hum Brain Mapp. 2024 Oct 15;45(15):e70029. doi: 10.1002/hbm.70029. Hum Brain Mapp. 2024. PMID: 39465912 Free PMC article.
-
Criticality of resting-state EEG predicts perturbational complexity and level of consciousness during anesthesia.bioRxiv [Preprint]. 2023 Oct 31:2023.10.26.564247. doi: 10.1101/2023.10.26.564247. bioRxiv. 2023. PMID: 37994368 Free PMC article. Preprint.
-
The evolution of whole-brain turbulent dynamics during recovery from traumatic brain injury.Netw Neurosci. 2024 Apr 1;8(1):158-177. doi: 10.1162/netn_a_00346. eCollection 2024. Netw Neurosci. 2024. PMID: 38562284 Free PMC article.
-
Virtual brain twins: from basic neuroscience to clinical use.Natl Sci Rev. 2024 Feb 28;11(5):nwae079. doi: 10.1093/nsr/nwae079. eCollection 2024 May. Natl Sci Rev. 2024. PMID: 38698901 Free PMC article. Review.
-
Critical dynamics in spontaneous EEG predict anesthetic-induced loss of consciousness and perturbational complexity.Commun Biol. 2024 Aug 5;7(1):946. doi: 10.1038/s42003-024-06613-8. Commun Biol. 2024. PMID: 39103539 Free PMC article.
References
-
- Ahlfors SP, Jones SR, Ahveninen J, Hämäläinen MS, Belliveau JW, Bar M. Direction of magnetoencephalography sources associated with feedback and feedforward contributions in a visual object recognition task. Neuroscience Letters. 2015;585:149–154. doi: 10.1016/j.neulet.2014.11.029. - DOI - PMC - PubMed
Publication types
MeSH terms
Grants and funding
LinkOut - more resources
Full Text Sources

