Calibrating agent-based models to tumor images using representation learning

Abstract

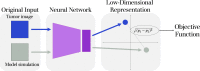
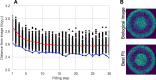
Agent-based models (ABMs) have enabled great advances in the study of tumor development and therapeutic response, allowing researchers to explore the spatiotemporal evolution of the tumor and its microenvironment. However, these models face serious drawbacks in the realm of parameterization - ABM parameters are typically set individually based on various data and literature sources, rather than through a rigorous parameter estimation approach. While ABMs can be fit to simple time-course data (such as tumor volume), that type of data loses the spatial information that is a defining feature of ABMs. While tumor images provide spatial information, it is exceedingly difficult to compare tumor images to ABM simulations beyond a qualitative visual comparison. Without a quantitative method of comparing the similarity of tumor images to ABM simulations, a rigorous parameter fitting is not possible. Here, we present a novel approach that applies neural networks to represent both tumor images and ABM simulations as low dimensional points, with the distance between points acting as a quantitative measure of difference between the two. This enables a quantitative comparison of tumor images and ABM simulations, where the distance between simulated and experimental images can be minimized using standard parameter-fitting algorithms. Here, we describe this method and present two examples to demonstrate the application of the approach to estimate parameters for two distinct ABMs. Overall, we provide a novel method to robustly estimate ABM parameters.

Fig 1. Schematic displaying how two inputs, a tumor image and the spatial output from an ABM simulation, are inputted into the same neural network and projected to low-dimensional space.

The Euclidean distance between these projected points is used as the objective function to be minimized with a parameter estimation algorithm.

Fig 2

Data-processing schematic (A) and example simulation (B). From the continuous spatial layout, cells are separated by property and discretized to a series of grids. The grids are then reduced to a smaller size, converting discrete locations to densities. In (B, left), pink dots are tumor cells (darker = higher PD-L1), teal dots are active T cells, and white are suppressed T cells. In (B, right), cell densities range from light pink to purple. For ease of visualization, we show the same size figures in the center and right panels, though we note there are fewer grid spaces in the right panel, compared to center.

Fig 3. Schematic displaying the initial estimation of parameter ranges.

The tumor image and the Monte Carlo simulations used for training the neural network are projected into low-dimensional space. Parameter values for the n closest simulations to the tumor image are compared and used to set the upper and lower bounds for parameter estimation.

Fig 4. Fitting results for Example 1.

(A) Fitting with a GA. Black dots–individuals in the GA. Red line–average fit. Blue line–best fit. (B) Visual comparison of the spatial layouts of the base simulation (top) and the best-fit simulation (bottom).

Fig 5. Fitting results for Example 2.

(A) Fitting with a GA. Black dots–individuals in the GA. Red line–average fit. Blue line–best fit. (B) Visual comparison of the processed image for the tumor image (top) and the best-fit simulation (bottom).