This is a preprint.
Altered Topological Structure of the Brain White Matter in Maltreated Children through Topological Data Analysis
- PMID: 37090232
- PMCID: PMC10120754
Altered Topological Structure of the Brain White Matter in Maltreated Children through Topological Data Analysis
Update in
-
Altered topological structure of the brain white matter in maltreated children through topological data analysis.Netw Neurosci. 2024 Apr 1;8(1):355-376. doi: 10.1162/netn_a_00355. eCollection 2024. Netw Neurosci. 2024. PMID: 38711544 Free PMC article.
Abstract
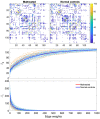
Childhood maltreatment may adversely affect brain development and consequently influence behavioral, emotional, and psychological patterns during adulthood. In this study, we propose an analytical pipeline for modeling the altered topological structure of brain white matter in maltreated and typically developing children. We perform topological data analysis (TDA) to assess the alteration in the global topology of the brain white-matter structural covariance network among children. We use persistent homology, an algebraic technique in TDA, to analyze topological features in the brain covariance networks constructed from structural magnetic resonance imaging (MRI) and diffusion tensor imaging (DTI). We develop a novel framework for statistical inference based on the Wasserstein distance to assess the significance of the observed topological differences. Using these methods in comparing maltreated children to a typically developing control group, we find that maltreatment may increase homogeneity in white matter structures and thus induce higher correlations in the structural covariance; this is reflected in the topological profile. Our findings strongly suggest that TDA can be a valuable framework to model altered topological structures of the brain. The MATLAB codes and processed data used in this study can be found at https://github.com/laplcebeltrami/maltreated.
Figures
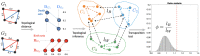
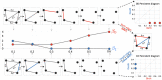

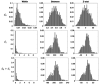
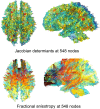


References
-
- Aber J. and Cicchetti D.. The socio-emotional development of maltreated children: An empirical and theoretical analysis. In Theory and Research in Behavioral Pediatrics: Volume 2, pages 147–205. Springer, 1984.
-
- Adams H., Emerson T., Kirby M., Neville R., Peterson C., Shipman P., Chepushtanova S., Hanson E., Motta F., and Ziegelmeier L.. Persistence images: A stable vector representation of persistent homology. Journal of Machine Learning Research, 18, 2017.
-
- Baer J. and Martinez C.. Child maltreatment and insecure attachment: A meta-analysis. Journal of reproductive and infant psychology, 24:187–197, 2006.
-
- Besthorn C., Sattel H., Geiger-Kabisch C., Zerfass R., and Förstl H.. Parameters of eeg dimensional complexity in alzheimer’s disease. Electroencephalography and clinical neurophysiology, 95(2):84–89, 1995. - PubMed
Publication types
Grants and funding
LinkOut - more resources
Full Text Sources
