Statistical learning of protein elastic network from positional covariance matrix

Abstract

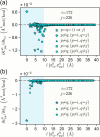
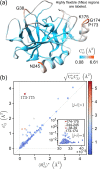
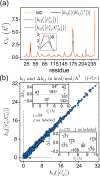
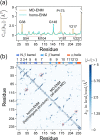
Positional fluctuation and covariance during protein dynamics are key observables for understanding the molecular origin of biological functions. A frequently employed potential energy function for describing protein structural variation at the coarse-gained level is elastic network model (ENM). A long-standing issue in biomolecular simulation is thus the parametrization of ENM spring constants from the components of positional covariance matrix (PCM). Based on sensitivity analysis of PCM, the direct-coupling statistics of each spring, which is a specific combination of position fluctuation and covariance, is found to exhibit prominent signal of parameter dependence. This finding provides the basis for devising the objective function and the scheme of running through the effective one-dimensional optimization of every spring by self-consistent iteration. Formal derivation of the positional covariance statistical learning (PCSL) method also motivates the necessary data regularization for stable calculations. Robust convergence of PCSL is achieved in taking an all-atom molecular dynamics trajectory or an ensemble of homologous structures as input data. The PCSL framework can also be generalized with mixed objective functions to capture specific property such as the residue flexibility profile. Such physical chemistry-based statistical learning thus provides a useful platform for integrating the mechanical information encoded in various experimental or computational data.

Keywords: All-atom molecular dynamics simulation; Elastic network model; Homologous structure; Positional covariance matrix; Serine protease; Statistical learning.

Graphical abstract

Fig. 1

The scheme of positional covariance statistical learning (PCSL) for computing the spring constant list [k_ij] of an elastic network model (ENM) from an ensemble of protein structures, $\{{\mathbf{r}}_i^I\}$.

Fig. 2

Sensitivities of positional fluctuations and covariances in ENM to a spring constant. The rat trypsin (RT) structure with the protein data bank ID 3TGI is used to construct the elastic network model of C_α carbons. The l_c cutoff for including an atom pair in the ENM is 10 Å, and every spring takes the same elastic constant value. For this zero^th-order ENM, magnitudes of positional fluctuations of node p and covariances of nodes p and q are ${\mathrm{C}}_{pp}^0$ and ${\mathrm{C}}_{pq}^0$, respectively. Variance of the inter-node distance is ${\hat{\mathrm{c}}}_{pq}^0$. The derivatives with respect to the k_ij between i = 172 and j = 226 are shown as an example. The center of geometry of the spring is ${\mathbf{r}}_{ij}^0$ and that of the node pair is ${\mathbf{r}}_{pq}^0$. The distance between the two centers is $l({\mathbf{r}}_{ij}^0,{\mathbf{r}}_{pq}^0)$. (a) $\partial {\mathrm{C}}_{pq}^0∕\partial k_{ij}$ versus $l({\mathbf{r}}_{ij}^0,{\mathbf{r}}_{pq}^0)$. (b) $\partial {\hat{\mathrm{c}}}_{pq}^0∕\partial k_{ij}$ versus $l({\mathbf{r}}_{ij}^0,{\mathbf{r}}_{pq}^0)$.

Fig. 3

Structure of the rat trypsin (RT) model system and the ${\mathrm{C}}_{ii}^{*}$, ${\hat{\mathrm{c}}}_{ij}^{*}$, and $⟨\delta l_{ij}^2{⟩}^{*}$ of C_α atoms in Ų calculated from the reference all-atom MD trajectory. (a) RT is a S1A serine protease family member and the 3TGI structure is shown in a ribbon representation. The color bar indicates the ${\mathrm{C}}_{ii}^{*}$ values. (b) For residue pairs of ∣j − i∣ > 1, the comparison of ${\hat{\mathrm{c}}}_{ij}^{*}$ with $⟨\delta l_{ij}^2{⟩}^{*}$. Insert: the comparison for neighboring residues of ∣j − i∣ = 1 with the same x- and y-axis.

Fig. 4

Calibration of PCSL in terms of the calculated spring constants and the predicted positional covariance. (a) The root-of-mean-squared (RMS) difference between $k_{ij}([{\hat{\mathrm{c}}}_{ij}^{*}])$, the spring constants learned from $[{\hat{\mathrm{c}}}_{ij}^{*}]$, and $k_{ij}([⟨\delta l_{ij}^2{⟩}^{*}])$, those learned from $[⟨\delta l_{ij}^2{⟩}^{*}]$, as a function of the data-regularization parameter ϵ. The RMS difference $\mathrm{\Delta }k([\hat{\mathrm{c}}{*}_{ij}],[⟨\delta l_{ij}^2{⟩}^{*}])$ is defined in Eq. (12). The left y-axis reports the value for ∣j − i∣ = 1 springs while the right y-axis is for the elastic parameters of ∣j − i∣ > 1. The insert is the scatter plot of $k_{ij}([{\hat{\mathrm{c}}}_{ij}^{*}])$ versus $k_{ij}([⟨\delta l_{ij}^2{⟩}^{*}])$ for the ∣j − i∣ > 1 springs. (b) The scatter plot of the C_ij value given by the ENM with the statistically learned spring constants and ${\mathrm{C}}_{ij}^{*}$, the targeted value. Color bar indicates the k_ij values for $l_{ij}^0<l_{\mathrm{c}}$.

Fig. 5

Comparison of PCSL with or without applying the additional scoring function for restraining the positional fluctuation profile by eq. (8) and eq. (9). Here, input data is the all-atom MD trajectory. (a) The C_ii profile predicted by the ENM of $k_{ij}([⟨\delta l_{ij}^2{⟩}^{*}])$ and of $k_{ij}([{\hat{\mathrm{c}}}_{ij}^{*}])$ does not involve the additional scoring function. The C_ii profile of the ENM of $k_{ij}([{\hat{\mathrm{c}}}_{ij}^{*},{\mathrm{C}}_{ii}^{*}])$ contains the scoring function for restraining the positional fluctuation profile. (b) The scatter plot of $k_{ij}([\hat{\mathrm{c}}{*}_{ij}],[\mathrm{C}{*}_{ii}])$ versus $k_{ij}([\hat{\mathrm{c}}{*}_{ij}])$ for ∣j − i∣ > 1 springs. The inserts show the change in spring constant Δk_ij due to the addition of ${\mathrm{C}}_{ii}^{*}$ restraints in PCSL for the springs of Y39 and K175.

Fig. 6

PCSL using an ensemble of homologous RT structures as input, homo-ENM, and the comparison with taking an all-atom MD trajectory as the targeted data, MD-ENM. In both cases, data regularization with ϵ = 0.6 (c.f. Methods) and restraint in residue flexibility profile with β = 0.7 (c.f. eq. (9)) are used. (a) The C_ii calculated from the homo-ENM and MD-ENM. The linked red boxes are examples of strongly coupled residue clusters. (b) The k_ij heat map of ∣j − i∣ > 1 springs for homo-ENM and MD-ENM. The red boxes are the residue clusters as those in (a). The RT secondary structures are highlighted on top. N-β barrel and C-β barrel are the N-terminal and C-terminal β barrel respectively. Numbers below are the sequential indices of β strands.

Fig. 7

PCSL for homo-ENM and MD-ENM shows specific mechanical hotspots. (a) The count of each residue in appearing in the exceptionally strong spring constants in homo-ENM and in MD-ENM. The count coming from the 42 common springs is in brown. Stacking on top of the common count is the count due to the exceptionally strong springs in homo-ENM but not in MD-ENM (pink), and that due to those in MD-ENM but not in homo-ENM (cyan). Residues are only labelled if the total count is higher than four in either model. The secondary structures can be referenced to Fig. 6b. (b) Illustration of the exceptionally strong springs and the mechanical hotspot residues in (a) on the protein structure in a ribbon representation. The coloring scheme follows that in (a). The residues and springs from the common category are made semi-transparent in the left and middle panel for clarity.