Quantum spin models for numerosity perception

Abstract

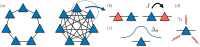
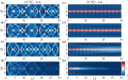
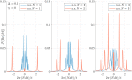
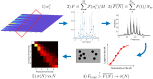
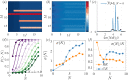
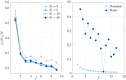
Humans share with animals, both vertebrates and invertebrates, the capacity to sense the number of items in their environment already at birth. The pervasiveness of this skill across the animal kingdom suggests that it should emerge in very simple populations of neurons. Current modelling literature, however, has struggled to provide a simple architecture carrying out this task, with most proposals suggesting the emergence of number sense in multi-layered complex neural networks, and typically requiring supervised learning; while simple accumulator models fail to predict Weber's Law, a common trait of human and animal numerosity processing. We present a simple quantum spin model with all-to-all connectivity, where numerosity is encoded in the spectrum after stimulation with a number of transient signals occurring in a random or orderly temporal sequence. We use a paradigmatic simulational approach borrowed from the theory and methods of open quantum systems out of equilibrium, as a possible way to describe information processing in neural systems. Our method is able to capture many of the perceptual characteristics of numerosity in such systems. The frequency components of the magnetization spectra at harmonics of the system's tunneling frequency increase with the number of stimuli presented. The amplitude decoding of each spectrum, performed with an ideal-observer model, reveals that the system follows Weber's law. This contrasts with the well-known failure to reproduce Weber's law with linear system or accumulators models.

Fig 1. Quantum spin model.

(a) Diagram of the spin system with variable connectivity, we present the case of nearest-neighbour and all-to-all coupling; (b) Diagramatic representation of the Hamiltonian and dissipative terms: each spin can propagate an excitation to its neighbours through the exchange term with amplitude J. Each spin experiences an energy offset given by the state of its neighbours. This energy shift is given by a gaussian profile centered in each spin with amplitude Δ₀, (c). Finally, each spin can interact with different dissipative channels, (d) leading to excitation losses and dephasing with a rate γ_i.

Fig 2. Magnetisation profiles.

(a) Evolution of the local magnetisation ${\sigma }_i^z$ for a system with M = 7 sites, J = 1, Δ₀ = 0, γ_l = 0 starting from a single excitation (spin up) on the middle site at t = 0 and nearest neighbor (n.n.) coupling. The dashed line highlights the magnetisation spreading in a light-cone manner; (b) same as (a) for ${\Delta }_0=0.1,\sigma =1/\sqrt{2}$; (c) same as (a) for ${\Delta }_0=0.1,\sigma =2/\sqrt{2}$; (d) same as (a) for γ_l = 0.1; (e)-(h) Same as (a)-(d) for the all-to-all (a.a.) case. In the n.n., we can observe that the excitation propagates in a light cone until reaching the boundaries, and then oscillates back and forth. The addition of interaction leads to space modulations that build over time changing quantitatively the magnetisation but without affecting the general behaviour. Inclusion of a spin decay rate γ_l ≠ 0 leads to the loss of the excitation over time. In contrast, the a.a. does not display any excitation cone and the spin up evenly spreads to all the neighbours and bounces back and forth with a constant frequency, including interaction we observe again the appearance of space modulation in the propagation profile.

Fig 3. Frequency spectrum of the magnetisation.

Amplitude spectrum of the magnetisation $\langle {\sigma }_i^z\rangle$ on site i = 5 as a function of time in a system with parameters M = 7 sites, $J=1,{\Delta }_0=0.1,\sigma =1/\sqrt{2},{\gamma }_l=0$ for varying number of spin flips during the evolution N = 1, 2, 3 displayed from left to right. In every panel we compare the results for the case of nearest-neighbours and all-to-all coupling, observing that the number of peaks and the overall behaviour of the spectrum shows small differences in the case of n.n., contrasting the a.a. case, where every time that a spin flip connects to a new magnetisation sector a new peak at a constant distance appears in the spectrum, showing the potential ability for the system to count. In both cases, the time domain used was 10 ≤ tJ ≤ 20 after the events occurring in sites i = 1, 3, 5 respectively at fixed times in the initial window between 0 ≤ tJ ≤ 10.

Fig 4. Agnostic estimation protocol summary.

(1) The local time signal of the magnetisation is registered in a chosen time window, after the excitations have entered the system; (2) The spectrum of the signal is computed and then averaged over the number M of sites in the network; (3) Averaging over realisations with excitations at random times, locations, and random angles produces a spectrum template for each numerosity; (4) Sample runs are then compared with the templates, using agnostic decoding; (5) The estimated errors are compared for different numerosities to assert whether the system follows the predicted Weber’s law.

Fig 5. Numerosity estimation in the quantum spin model.

(a) Example magnetisation profile from one of the sampled trajectories for the case of M = 18 spins and N = 4 random spin flips, with Δ₀ = 0, γ_l = 0. (b) Average magnetisation for the same system for a set of N_t = 200 trajectories. As the events have random location and intensity, there is no information in the averaged time signal. (c) Average of the amplitude spectrum of the magnetisation signals in the time window between $t=(8J,18+\sqrt{2}J)$: the spectra were computed over individual trajectories and sites, then spaced averaged, and finally trajectory averaged. Here we display only the positive frequencies. (d) Psychometric function results for the quantum spin model with M = 18, and same parameters as in the top panel, where N spin flips random in location, time, and rotation angle, have occurred before registering the magnetisation. (e) Corresponding standard deviation estimates from the fits of the psychometric functions on the left. Here, we compare the previous case where each event is a spin flip of random amplitude (orange) with a case where the rotations where again random but their sum was constrained to be equal to 3π (blue). (f) Weber fraction associated to the results in the middle panel.

Fig 6. Decoder validation.

(a) Weber fraction associated to the decoding of numerosity for the magnetisation signals with random amplitude excitations (RR) in Fig 5, for varying number of trajectories N_t = 3, 5, 10, 40 with which we construct our library templates. We observe that the decoding converges with a very limited number of samples. (b) Weber fraction associated to the frequency decoding for sinusoidal activation maps with frequency ranging from f = 1 − 18, both noiseless and with noise proportional to the inverse of the frequency. We show that the decoder does not incorporate additional noise to the analysis by comparing the performance of both classical signals.