Fidelity of hyperbolic space for Bayesian phylogenetic inference

Abstract

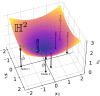
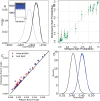
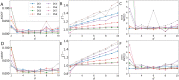
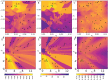
Bayesian inference for phylogenetics is a gold standard for computing distributions of phylogenies. However, Bayesian phylogenetics faces the challenging computational problem of moving throughout the high-dimensional space of trees. Fortunately, hyperbolic space offers a low dimensional representation of tree-like data. In this paper, we embed genomic sequences as points in hyperbolic space and perform hyperbolic Markov Chain Monte Carlo for Bayesian inference in this space. The posterior probability of an embedding is computed by decoding a neighbour-joining tree from the embedding locations of the sequences. We empirically demonstrate the fidelity of this method on eight data sets. We systematically investigated the effect of embedding dimension and hyperbolic curvature on the performance in these data sets. The sampled posterior distribution recovers the splits and branch lengths to a high degree over a range of curvatures and dimensions. We systematically investigated the effects of the embedding space's curvature and dimension on the Markov Chain's performance, demonstrating the suitability of hyperbolic space for phylogenetic inference.

Fig 1. Hyperbolic embedding of eight taxa.

Eight points (taxa) lie on a two-dimensional hyperboloid sheet ${\mathbb{H}}^2$ in ${\mathbb{R}}^3$. Arrows indicate how each two-dimensional point (x₁, x₂) is deterministically projected up onto the sheet by ϕ. The green dashed line illustrates that the distance between two taxa is the length of the geodesic on the hyperboloid surface.

Fig 2. Comparison between MrBayes and Dodonaphy’s MCMC starting from the evolutionary distances.

Comparison of (a) posterior probability trace, (b) split frequencies with 95% confidence intervals (CI), (red dots: MrBayes value not covered by CI), (c) mean branch lengths (leaf edges in blue circles, internal edges in red diamonds), (d) total tree length estimation of 10 repeats. Markers in (c) are shaded by the frequency of appearance in the golden run. In (a, d) black lines show the two MrBayes runs and thin blue lines show Dodonaphy’s results.

Fig 3. Effect of embedding curvature on the posterior distribution.

Comparison to the true posterior of: a) ASDSF, b) relative difference in median tree length, c) relative difference in the variance of tree length. The truncated variance ratio for DS5 is approximately zero. The right side corresponds to flatter (and Euclidean) curvature (κ = 0 gives log₁₀(−κ) = −∞) and the left side is more curved.

Fig 4. Effect of embedding dimension on the posterior distribution.

Comparison to the true posterior of: a, d) ASDSF, b, e) relative difference in median tree length, c, f) relative difference in the variance of tree length. Top row curvature κ = −1, bottom row κ = −100. Truncated variance ratio in c) for DS3 with d = 2 is 16.41 and 39.05 for DS7.

Fig 5. Heat map of the decoded tree’s properties.

Obtained by a grid search in ${\mathbb{H}}^2$, moving one node (green diamond) through embedding space. a, d) joint probability p(T, Y), b, e) symmetric difference from best tree topology and c, f) total length. Top row curvature κ = −1 and bottom row κ = −1000. Black dots are the fixed locations of the remaining nodes.

Fig 6. SPR distances of samples about an embedded tree.

SPR distance of trees sampled from a Multivariate Gaussian (covariance Σ × I) about a tree containing 100 leaves embedded in ${\mathbb{H}}^3$ with curvature κ = −1. Distributions are estimated from 2000 samples.