Parabolic-Gaussian Double Quantum Wells under a Nonresonant Intense Laser Field

Abstract

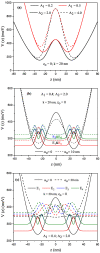
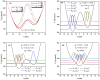
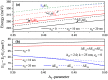
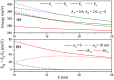
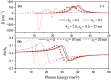
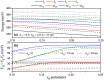
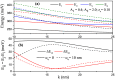
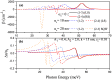
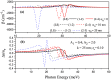
In this paper, we investigate the electronic and optical properties of an electron in both symmetric and asymmetric double quantum wells that consist of a harmonic potential with an internal Gaussian barrier under a nonresonant intense laser field. The electronic structure was obtained by using the two-dimensional diagonalization method. To calculate the linear and nonlinear absorption, and refractive index coefficients, a combination of the standard density matrix formalism and the perturbation expansion method was used. The obtained results show that the electronic and thereby optical properties of the considered parabolic-Gaussian double quantum wells could be adjusted to obtain a suitable response to specific aims with parameter alterations such as well and barrier width, well depth, barrier height, and interwell coupling, in addition to the applied nonresonant intense laser field.

Keywords: double quantum well; intense laser field; parabolic–Gaussian potential.

Figure 1

Parabolic–Gaussian symmetric DQW ($z_o=0$) potential for a constant value of k(=20 nm) versus the z-coordinate. Parabolic–Gaussian symmetric DQW, solid (dashed) curves are for $A_2=2.0$ $(A_2=4.0)$ and black (red) curves $A_1=0.2$ $(A_1=0.5)$ (a), Parabolic–Gaussian symmetric DQW confinement profiles and squared modulus of the wave-functions corresponding to the first 4 energy levels for ${\alpha }_o=0$ (solid curves) and ${\alpha }_o=10 \mathrm{nm}$ (dashed curves) (b), and Parabolic–Gaussian symmetric DQW potential and squared modulus of the wave-functions corresponding to the first 4 energy levels for ${\alpha }_o=0$ (solid curves) and ${\alpha }_o=20 \mathrm{nm}$ (dashed curves) (c). Results are for $k=20 \mathrm{nm}$, $A_1=0.4$ and $A_2=2.0$.

Figure 2

(a) Parabolic–Gaussian asymmetric DQW confinement profiles for the parameters of $k=20 \mathrm{nm}$, $A_1=0.5$, $A_2=2.0$ (solid curves) and $A_2=4.0$ (dashed curves) and for two different $z_o$ values, black (red) curve is for $z_o=0.15$ $(z_o=0.30)$, parabolic–Gaussian asymmetric DQW potential and squared modulus of the wave functions corresponding to the first four energy levels for (b) ${\alpha }_o=0$, (c) ${\alpha }_o=10 \mathrm{nm}$, and (d) ${\alpha }_o=20 \mathrm{nm}$. The results in Figure 2b–d are for $z_o=0.10$, $k=15 \mathrm{nm}$, $A_1=0.4$, $A_2=2.0$.

Figure 3

For $k=25 \mathrm{nm}$, $A_2=2.0$, $z_o=0$, (a) changes in the energies of the electron confined within parabolic–Gaussian symmetric DQW under the intense laser field versus parameter $A_1$; (b) variation of energy differences between related levels versus the $A_1$ parameter. Solid, dashed, and dotted curves are for ${\alpha }_o=0$, ${\alpha }_o=10 \mathrm{nm}$, and ${\alpha }_o=20 \mathrm{nm}$, respectively.

Figure 4

For $A_1=0.4$, $A_2=2.0$ and $z_o=0$, (a) changes in the energies of the electron confined within parabolic–Gaussian symmetric DQW under the intense laser field versus the k parameter; (b) variation of energy differences between related levels versus the k parameter. Solid and dashed curves are for ${\alpha }_o=0$ and ${\alpha }_o=10 \mathrm{nm}$, respectively.

Figure 5

For $k=25 \mathrm{nm}$, $A_2=2.0$ and $z_o=0$, (a) variation in the total absorption coefficient versus the photon energy corresponding to the (2-3) transition in parabolic–Gaussian symmetric DQW; (b) variation in the total refractive index versus the photon energy, where black (red) curves are for $A_1=0.4$ $(A_1=0.5)$ and solid, dashed, and dotted curves are for ${\alpha }_o=0$, ${\alpha }_o=10 \mathrm{nm}$, and ${\alpha }_o=20 \mathrm{nm}$, respectively.

Figure 6

For the transitions between energy levels in parabolic–Gaussian symmetric DQW with parameters $z_o=0$, $A_1=0.4$ and $A_2=2.0$, (a) change in total absorption coefficients versus the photon energy; (b) variation in the total refractive index versus the photon energy, where black (red) curves are for $k=25 \mathrm{nm}$ $(k=15 \mathrm{nm})$ and solid, dashed, and dotted curves are for ${\alpha }_o=0$, ${\alpha }_o=10 \mathrm{nm}$, and ${\alpha }_o=20 \mathrm{nm}$, respectively.

Figure 7

For $A_1=0.5$ and $A_2=2.0$ and $k=25 \mathrm{nm}$, (a) variations in the first four lowest energy levels of the electron confined within parabolic–Gaussian asymmetric DQW under an intense laser field with respect to the $z_o$ parameter; (b) variation in energy differences between some levels versus the $z_o$ parameter. Solid, dashed, and dotted curves are for ${\alpha }_o=0$, ${\alpha }_o=10 \mathrm{nm}$, and ${\alpha }_o=20 \mathrm{nm}$, respectively.

Figure 8

For $A_1=0.4$ and $A_2=2.0$ and $z_o=0.10$, (a) changes of the first four lowest energy levels of electron confined within parabolic–Gaussian asymmetric DQW under the intense laser field versus the k-parameter; (b) variation in energy differences between some levels versus the k parameter. Solid and dashed curves are for ${\alpha }_o=0$ and ${\alpha }_o=10 \mathrm{nm}$, respectively.

Figure 9

For some transitions in parabolic–Gaussian asymmetric DQW with $k=15 \mathrm{nm}$, $z_o=0.10$, $A_1=0.4$ and $A_2=2.0$. (a) Variation in total absorption coefficients versus photon energy; (b) variation in total refractive index versus photon energy. Solid, dashed, and dotted curves are for ${\alpha }_o=0$, ${\alpha }_o=10 \mathrm{nm}$, and ${\alpha }_o=20 \mathrm{nm}$, respectively.

Figure 10

For some transitions in parabolic–Gaussian asymmetric DQW with $k=25 \mathrm{nm}$, $z_o=0.10$, $A_1=0.4$ and $A_2=2.0$. (a) Variation in the total absorption coefficients concerning photon energy; (b) variation in total refractive index concerning photon energy. Solid, dashed, and dotted curves are for ${\alpha }_o=0$, ${\alpha }_o=10 \mathrm{nm}$, and ${\alpha }_o=20 \mathrm{nm}$, respectively.