Algorithm for optimized mRNA design improves stability and immunogenicity

Abstract

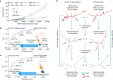
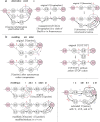
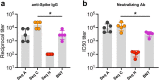
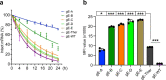
Messenger RNA (mRNA) vaccines are being used to combat the spread of COVID-19 (refs. ^1-3), but they still exhibit critical limitations caused by mRNA instability and degradation, which are major obstacles for the storage, distribution and efficacy of the vaccine products⁴. Increasing secondary structure lengthens mRNA half-life, which, together with optimal codons, improves protein expression⁵. Therefore, a principled mRNA design algorithm must optimize both structural stability and codon usage. However, owing to synonymous codons, the mRNA design space is prohibitively large-for example, there are around 2.4 × 10⁶³² candidate mRNA sequences for the SARS-CoV-2 spike protein. This poses insurmountable computational challenges. Here we provide a simple and unexpected solution using the classical concept of lattice parsing in computational linguistics, where finding the optimal mRNA sequence is analogous to identifying the most likely sentence among similar-sounding alternatives⁶. Our algorithm LinearDesign finds an optimal mRNA design for the spike protein in just 11 minutes, and can concurrently optimize stability and codon usage. LinearDesign substantially improves mRNA half-life and protein expression, and profoundly increases antibody titre by up to 128 times in mice compared to the codon-optimization benchmark on mRNA vaccines for COVID-19 and varicella-zoster virus. This result reveals the great potential of principled mRNA design and enables the exploration of previously unreachable but highly stable and efficient designs. Our work is a timely tool for vaccines and other mRNA-based medicines encoding therapeutic proteins such as monoclonal antibodies and anti-cancer drugs^7,8.

Fig. 1. Overview of mRNA coding region design for both stability and codon optimality using SARS-CoV-2 spike protein as an example.

a, Due to codon degeneracy and combinatorial explosion, there are around 2.4 × 10⁶³² possible mRNA sequences encoding the spike protein. Enumerating every possible sequence would take around 10⁶¹⁶ billion years. The pink and blue paths represent the wild-type and the optimally stable (lowest free energy) sequences, respectively. nt, nucleotides. b, The secondary structures of wild-type (left) and optimally stable (right) spike mRNAs. The wild-type mRNA is mostly single-stranded and thus prone to degradation in loop regions (red), whereas the optimally stable mRNA is mostly double-stranded. Optimization using LinearDesign takes around 11 min. c, The application of DFA and lattice parsing in computational linguistics (left) and its adaptation to mRNA design (right). An mRNA DFA (analogous to a word lattice) compactly encodes all mRNA candidates, which are folded simultaneously by lattice parsing to find the optimal mRNA (Fig. 2). d, Two-dimensional visualization of the mRNA design space, with stability (represented by MFE) on the x axis and codon optimality (represented by CAI) on the y axis. The standard mRNA design method of codon optimization improves codon usage (pink arrow) but is unable to explore the high-stability region (left of the dashed line); this standard approach is exemplified by the COVID-19 mRNA vaccine products BNT-162b2 (BioNTech-Pfizer, circle), mRNA-1273 (Moderna, star) and CVnCoV/CV2CoV (CureVac, wedge). LinearDesign jointly optimizes stability and codon optimality (blue curve, with λ being the weight assigned to codon optimality). We selected seven mRNA designs (four (A–D) are shown here) and a codon-optimized baseline (H) for in vitro and in vivo experiments (Fig. 4).

Fig. 2. Illustration of the LinearDesign algorithm.

a, Codon DFAs. b, An mRNA DFA (bottom) and lattice parsing on that DFA (top). In the DFA, the optimal mRNA sequence under a simplified energy model is shown as the blue path, together with its optimal structure shown in the dot-bracket format (dots indicate unpaired, and brackets indicate base pairs). In lattice parsing, the brown and black arcs also depict base pairs (two GC pairs and two AU pairs), and the trapezoidal shaded areas depict the decomposition of the optimal structure. Among all mRNA sequences encoded in the DFA, lattice parsing finds the optimal sequence with its optimal structure, achieving the lowest free energy under this energy model, where GC and AU pairs have energies of −3 and −2 kcal mol⁻¹, respectively (Extended Data Fig. 1e). Note that here we use the simplified energy model for illustration, but our implementation uses the nearest-neighbour energy model. c, Another illustration of the optimal sequence and secondary structure in b. d, Joint optimization between stability and codon optimality by integrating the codon optimality in weighted DFAs. Top, the codon frequencies for threonine and serine. The relative adaptiveness w(c) of a codon c is the ratio of the frequency of c to the frequency of the most frequent codon encoding the same amino acid (white bar), and its value is shown to the right of the bars. Bottom, a weighted mRNA DFA encodes the CAI of each candidate in the total weight of its corresponding path by using –log[w(c)] (the cost of choosing codon c) as edge weights (Methods, ‘Optimization objectives’). This weighted DFA is used as input to lattice parsing for joint optimization between stability and codon optimality.

Fig. 3. Computational characteristics of the LinearDesign algorithm.

a, Runtime analysis of mRNA design for proteins in UniProt (Supplementary Table 1). Overall, our exact search scales quadratically with sequence length (Supplementary Figs. 7 and 8), and our MFE + CAI mode (with λ = 4) is about 15% slower than the MFE-only version. Moreover, beam search (b = 500) significantly speeds up the design of long sequences, with minor search errors (Supplementary Fig. 9). b,c, Two-dimensional (MFE–CAI) visualizations of designs for the SARS-CoV-2 spike (b) and VZV gE (c) proteins, respectively (both using human codon preference). The blue curves form the feasibility limit (optimal boundary), by varying λ from 0 to ∞ (see Extended Data Fig. 4 for λ of (–∞, 0]). The GC percentage is shown in parentheses. The human genome favours GC-rich codons; therefore, codon optimization (pink arrows) also improves stability, but only marginally, as the two optimization directions (codon versus stability) are largely orthogonal. By contrast, with an AU-rich codon preference (such as in yeast), codon optimization decreases stability (Extended Data Fig. 4b). d, Secondary structures of the mRNA designs for SARS-CoV-2 spike and VZV gE protein. The optimal-CAI designs (top, λ = ∞) are largely single-stranded (around 60% base-paired), whereas the optimally stable designs (bottom, λ = 0) are mostly double-stranded (around 80% base-paired). We also show intermediate designs (centre, λ = 4) with a balance of stability and CAI.

Fig. 4. Experimental evaluation of LinearDesign-generated mRNA sequences encoding SARS-CoV-2 spike protein.

a, Summary of chemical stability of and protein expression from spike mRNA designs A–G and the corresponding immune response (induction of anti-spike IgG) in mice compared to the codon-optimized benchmark H. The vaccines of mRNA-1273 and BNT-162b2 are annotated with daggers, because they use modified nucleotides, but their MFEs here are calculated with the standard energy model. b, Non-denaturing agarose gel characterization of mRNA, showing the correlation of gel mobility with minimum free energy. For gel source data, see Supplementary Fig. 1a. c, Chemical stability of mRNAs upon incubation in 10 mM Mg²⁺ buffer at 37 °C. Data are from three independent experiments. Seq., sequence. d, Protein expression levels from mRNAs 48 h after transfection into HEK293 cells, as determined by flow cytometry. Mean fluorescence intensity (MFI) values are derived from three independent experiments. Kruskal–Wallis ANOVA with Dunn’s multiple comparisons with the H group. e–g, C57BL/6 mice (n = 6) were immunized intramuscularly with two doses of formulated mRNA with a two-week interval. e, End-point titre of anti-spike IgG. f, Levels of neutralizing antibodies against wild-type SARS-CoV-2. IC₅₀, half-maximal inhibitory concentration. g, Frequencies of IFNγ-secreting T cells, measured by enzyme-linked immunospot (ELISpot) assay. Two-tailed Mann–Whitney U test. Data are mean ± s.d. (c,d), geometric mean ± geometric s.d. (e,f) or mean ± s.e.m. (g). *P < 0.05, **P < 0.01, ***P < 0.001. NS, not significant. See Extended Data Figs. 5–7 and Supplementary Figs. 10 and 12 for extra experimental results and predicted secondary structures, and Supplementary Table 2 for detailed computational and experimental data. Source Data

Fig. 5. Experimental evaluation of LinearDesign-generated mRNAs encoding VZV gE protein.

a, Summary of chemical stability of and protein expression from VZV gE mRNA designs and the corresponding immune response (induction of anti-gE IgG) in mice. The ‘sweet spot’ region is highlighted with light blue shading. b, Non-denaturing agarose gel characterization of mRNA showing the correlation of gel mobility with minimum free energy; for gel source data, see Supplementary Fig. 1b. c, Chemical stability of mRNAs upon incubation in 10 mM Mg²⁺ buffer at 37 °C. Data are from three independent experiments. d, Protein expression levels from mRNAs 48 h after transfection into HEK293 cells, as determined by flow cytometry. MFI values are derived from three independent experiments. Kruskal–Wallis ANOVA with Dunn’s multiple comparisons with the gE-Ther group. e, C57BL/6 mice (n = 5) were immunized intramuscularly with two doses of formulated mRNA with a two-week interval. End-point titre of anti-gE IgG is shown. Two-tailed Mann–Whitney U test. Data are mean ± s.d. (c,d) or geometric mean ± geometric s.d. (e). See Extended Data Fig. 8 for extra experimental results, Supplementary Fig. 11 for predicted secondary structures and Supplementary Table 3 for detailed computational and experimental data. Source Data

Extended Data Fig. 1. Illustrations of the optimization problems in mRNA design, DFA representations, single sequence folding as natural language parsing, and lattice parsing.

a–b, Visualization of mRNA design as optimization problems for stability (objective 1, in a) and joint stability and codon optimality (objectives 1 and 2, in b). c–h show how lattice parsing solves the first optimization problem (see Fig. 2d for the second). c, Codon DFAs. d, An mRNA DFA made of three codon DFAs. The thick paths depict the optimal mRNA sequences under the simplified energy model in e, AUGCU⋆UGA, where ⋆ could be any nucleotide. e, Stochastic context-free grammar (SCFG) for a simplified folding free energy model. Each rule has a cost (i.e., energy term, the lower the better), and the dotted arcs represent base pairs in RNA secondary structure. f, Single-sequence folding is equivalent to context-free parsing with an SCFG; the parse tree represents the best secondary structure for the input mRNA sequence. g, We extend single-sequence parsing (top) to lattice parsing (bottom) by replacing the input string with a DFA, where each string index becomes a DFA state, and a span becomes a path between two states. h, Lattice parsing with the grammar in e for the DFA in d. The blue arcs below the DFA depict the (shared) best structure for the optimal sequences AUGCU⋆UGA in the whole DFA, while the dashed light-blue arcs above the DFA represent the best structure for a suboptimal sequence AUGUUAUAA. Lattice parsing can also incorporate codon optimality (objective 2, see b), by replacing the DFA with a weighted one (Fig. 2d).

Extended Data Fig. 2. Word lattice and lattice parsing in natural language processing, and correspondence between linguistics and biology.

a, An example of word lattice (sentence DFA) for speech recognition. b, Simplified language grammar. c, Single sentence parsing with between-word indices, which is a special case of word lattice parsing. d, Illustration of word lattice parsing for speech recognition with given word lattice and language grammar; the dashed blue arcs above the DFA depict the best parsing structure for the optimal sentence “I like this meal”, while the dashed light-blue arcs below the DFA represent the best parsing structure for a non-optimal sentence “alike this veal”. e, Correspondence between computational linguistics (left) and computational biology (right). See also Fig. 1.

Extended Data Fig. 3. Examples of the DFA representations for extended codons, modified nucleotides, and coding constraints.

a, Alternative genetic codes of serine, tryptophan, and threonine. b, Avoiding certain codon. On the left it shows the original DFA of serine (up), in which the red dashed arrows indicating UCA and UCG are chosen to be avoided, resulting in a new DFA (down). On the right it shows removing the rare amber STOP codon (UAG). c, Avoiding a specific adjacent codon pair. d, Extended serine DFA can include chemically modified nucleotides pseudouridine (Ψ), 6-Methyladenosine (m⁶A) and 5-methylcytosine (m⁵C).

Extended Data Fig. 4. Two dimensional (MFE-CAI) visualizations of mRNA designs for the Spike protein using human codon preference (a) and yeast codon preference (b) with positive and negative λ’s.

GC% are shown in parentheses. The human genome prefers GC-rich codons that lead to higher CAI designs are with higher GC%, while the yeast genome prefers AU-rich codons that exhibit an opposite relationship between CAI and GC%. See also Fig. 3 for more in silico results of LinearDesign.

Extended Data Fig. 5. Extra experimental results of LinearDesign-generated mRNAs encoding the Spike protein.

a, In-solution stability of sequences A–H in PBS buffer containing 20 mM Mg²⁺ at 37 °C over the course of 24 h. The degradation experiments were performed in triplicate independently and the data were presented as mean ± s.d. and fitted with a one-phase decay curve. b, Protein expression of mRNAs following transfection into HEK293 cells for 24 h was determined by flow cytometry. MFI values derived from three independent experiments are shown. Kruskal–Wallis analysis of variance (ANOVA) with Dunn’s multiple comparisons test to H group was performed for statistical analysis. ***P < 0.001. See Fig. 4c, d for similar experiments but with 10 mM Mg²⁺ and 48 h, respectively.

Extended Data Fig. 6. In-solution stability and protein expression of sequences A, C, H and BNT, for a head-to-head in vitro comparison between LinearDesign and BioNTech-Pfizer mRNA sequences.

a-b, In-solution stability of mRNAs in PBS buffer containing 20 mM Mg²⁺ or 10 mM Mg²⁺ at 37 °C. Data are from three independent experiments and were presented as mean ± s.d. and fitted with one-phase decay curve. c-d, Protein expression of mRNAs was determined 24 h or 48 h following transfection into HEK293 cells. MFI value is presented as mean ± s.d. Each group has three independent assays and 10,000 live cells were collected for analysis in each assay. Kruskal–Wallis analysis of variance (ANOVA) with Dunn’s multiple comparisons test to BNT group was performed for statistical analysis. **P < 0.01, ***P < 0.001.

Extended Data Fig. 7. Antibody (Ab) responses induced by sequences A, C, H and BNT-based mRNA vaccines, for a head-to-head in vivo comparison between LinearDesign and BioNTech-Pfizer mRNA sequences.

C57BL/6 mice (n = 5) were immunized i.m. with two doses of mRNA vaccines at a 2-week interval. Seven days after boost immunization, levels of anti-Spike IgG (a) and neutralizing Abs (b) against pseudotyped SARS-CoV-2 were measured. Data were presented as geometric mean ± geometric s.d. A two-tailed Mann-Whitney U test was used for statistical analysis. *P < 0.05. See Source Data for details. Source Data

Extended Data Fig. 8. Extra stability and protein expression results of LinearDesign-generated mRNAs encoding VZV gE protein.

a, In-solution stability of mRNAs upon incubation in buffer (Mg²⁺ = 20 mM) at 37 °C. Percentage of intact mRNA is shown. Data are presented as mean ± SD from three independent experiments. b, Protein expression of mRNAs following transfection into HEK293 cells for 24 h was determined by flow cytometry. Each group has three independent assays and 10,000 live cells were collected for analysis in each assay. MFI value is presented as mean ± s.d. Kruskal–Wallis analysis of variance (ANOVA) with Dunn’s multiple comparisons test to gE-Ther group was performed for statistical analysis. *P < 0.05, ***P < 0.001.