Distribution of mutation rates challenges evolutionary predictability
- PMID: 37134005
- PMCID: PMC10268835
- DOI: 10.1099/mic.0.001323
Distribution of mutation rates challenges evolutionary predictability
Abstract
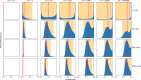
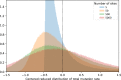
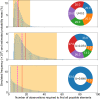
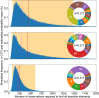
Natural selection is commonly assumed to act on extensive standing genetic variation. Yet, accumulating evidence highlights the role of mutational processes creating this genetic variation: to become evolutionarily successful, adaptive mutants must not only reach fixation, but also emerge in the first place, i.e. have a high enough mutation rate. Here, we use numerical simulations to investigate how mutational biases impact our ability to observe rare mutational pathways in the laboratory and to predict outcomes in experimental evolution. We show that unevenness in the rates at which mutational pathways produce adaptive mutants means that most experimental studies lack power to directly observe the full range of adaptive mutations. Modelling mutation rates as a distribution, we show that a substantially larger target size ensures that a pathway mutates more commonly. Therefore, we predict that commonly mutated pathways are conserved between closely related species, but not rarely mutated pathways. This approach formalizes our proposal that most mutations have a lower mutation rate than the average mutation rate measured experimentally. We suggest that the extent of genetic variation is overestimated when based on the average mutation rate.
Keywords: Pseudomonas; coupon collector's problem; distribution of mutation rates; mutation bias; mutation rate; predicting evolution.
Conflict of interest statement
The authors declare no competing interests.
Figures
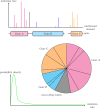

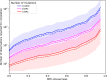
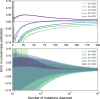

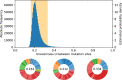




Similar articles
-
Predicting mutational routes to new adaptive phenotypes.Elife. 2019 Jan 8;8:e38822. doi: 10.7554/eLife.38822. Elife. 2019. PMID: 30616716 Free PMC article.
-
Low mutational load and high mutation rate variation in gut commensal bacteria.PLoS Biol. 2020 Mar 10;18(3):e3000617. doi: 10.1371/journal.pbio.3000617. eCollection 2020 Mar. PLoS Biol. 2020. PMID: 32155146 Free PMC article.
-
Adaptive evolution by recombination is not associated with increased mutation rates in Maize streak virus.BMC Evol Biol. 2012 Dec 27;12:252. doi: 10.1186/1471-2148-12-252. BMC Evol Biol. 2012. PMID: 23268599 Free PMC article.
-
The Role of Mutation Bias in Adaptive Evolution.Trends Ecol Evol. 2019 May;34(5):422-434. doi: 10.1016/j.tree.2019.01.015. Trends Ecol Evol. 2019. PMID: 31003616 Review.
-
How does adaptation sweep through the genome? Insights from long-term selection experiments.Proc Biol Sci. 2012 Dec 22;279(1749):5029-38. doi: 10.1098/rspb.2012.0799. Epub 2012 Jul 25. Proc Biol Sci. 2012. PMID: 22833271 Free PMC article. Review.
Cited by
-
Mutation bias and adaptation in bacteria.Microbiology (Reading). 2023 Nov;169(11):001404. doi: 10.1099/mic.0.001404. Microbiology (Reading). 2023. PMID: 37943288 Free PMC article. Review.
-
Extending evolutionary forecasts across bacterial species.Proc Biol Sci. 2024 Dec;291(2036):20242312. doi: 10.1098/rspb.2024.2312. Epub 2024 Dec 11. Proc Biol Sci. 2024. PMID: 39657800 Free PMC article.
-
Antimutator and Mutational Spectrum Effects Can Combine to Reduce Evolutionary Potential in Escherichia coli ΔnudJ.Mol Biol Evol. 2025 Jul 30;42(8):msaf182. doi: 10.1093/molbev/msaf182. Mol Biol Evol. 2025. PMID: 40729517 Free PMC article.
References
-
- Stoltzfus A. Mutation, Randomness, and Evolution. Oxford University Press; 2021. - DOI
Publication types
MeSH terms
LinkOut - more resources
Full Text Sources

