Acoustic stability of a self-gravitating cylinder leading to astrostructure formation

Abstract

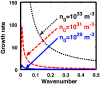
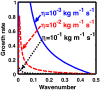
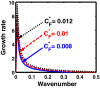
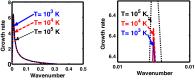
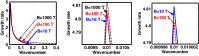
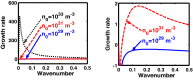
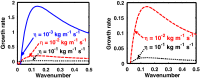
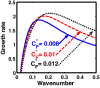
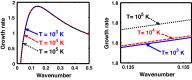
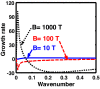
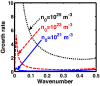
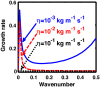
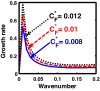
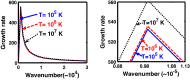
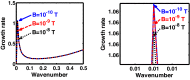
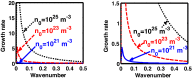
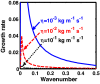
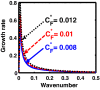
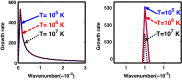
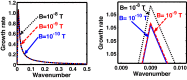
We employ a quantum hydrodynamic model to investigate the cylindrical acoustic waves excitable in a gyromagnetoactive self-gravitating viscous cylinder comprised of two-component (electron-ion) plasma. The electronic equation of state incorporates the effect of temperature degeneracy. It reveals an expression for the generalized pressure capable of reproducing a completely degenerate (CD) quantum (Fermi) pressure and a completely non-degenerate (CND) classical (thermal) pressure. A standard cylindrical wave analysis, moderated by the Hankel function, yields a generalized linear (sextic) dispersion relation. The low-frequency analysis is carried out procedurally in four distinct parametric special cases of astronomical importance. It includes the quantum (CD) non-planar (cylindrical), quantum (CD) planar, classical (CND) non-planar (cylindrical), and classical (CND) planar. We examine the multi-parametric influences on the instability dynamics, such as the plasma equilibrium concentration, kinematic viscosity, and so forth. It is found that, in the quantum regime, the concentration plays a major role in the system destabilization. In the classical regime, the plasma temperature plays an important role in both the stabilization and destabilization. It is further seen that the embedded magnetic field influences the instability growth dynamics in different multiparametric regimes extensively, and so forth. The presented analysis can hopefully be applicable to understand the cylindrical acoustic wave dynamics leading actively to the formation of astrophysical gyromagnetic (filamentary) structures in diverse astronomical circumstances in both the classical and quantum regimes of astronomical relevance.

Figure 1

Profile of the normalized growth rate $\left({\mathrm{\Omega }}_i\right)$ with variation in the normalized wavenumber $\left(k^{\ast }\right)$. The different lines link to different values of the equilibrium number density $\left(n_0\right)$ in non-planar (cylindrical) geometry in the quantum regime ($ħ\ne 0$).

Figure 2

Same as Fig. 1, but for different values of the normalized kinematic viscosity $\left({\eta }^{\ast }\right)$.

Figure 3

Same as Fig. 1, but for different values of the normalized Coriolis rotational force $\left(C_F^{\ast }\right)$.

Figure 4

Same as Fig. 1, but for different values of the normalized thermal temperature $\left(T^{\ast }\right)$. The second subplot is the magnified version depicting the peaks (kinks) clearly.

Figure 5

Same as Fig. 1, but for different values of magnetic field $\left(B\right)$. The two subsequent subplots depict the magnified versions clearly highlighting the peaks (kinks).

Figure 6

Profile of the normalized growth rate $\left({\mathrm{\Omega }}_i\right)$ with variation in the normalized wavenumber $\left(k^{\ast }\right)$. The different lines link to different values of the equilibrium number density $\left(n_0\right)$ in planar (non-cylindrical) geometry in the quantum regime. The second subplot is the enlarged version highlighting the trends for $n_0={10}^{29}$ m^-3 and $n_0={10}^{31}$ m^-3.

Figure 7

Same as Fig. 6, but for different values of the normalized kinematic viscosity $\left({\eta }^{\ast }\right)$. The second subplot is the enlarged version clearly highlighting the trends for $\eta ={10}^{-2}$ kg m^-1 s^-1 and $\eta ={10}^{-1}$ kg m^-1 s^-1.

Figure 8

Same as Fig. 6, but for different values of the normalized Coriolis rotational force $\left(C_F^{\ast }\right)$.

Figure 9

Same as Fig. 6, but for different values of the normalized thermal temperature $\left(T^{\ast }\right)$. The second subplot is the magnified version depicting the peaks clearly.

Figure 10

Same as Fig. 6, but for different values of the magnetic field $\left(B\right)$.

Figure 11

Profile of the normalized growth rate $\left({\mathrm{\Omega }}_i\right)$ with variation in the normalized wavenumber $\left(k^{\ast }\right)$. The different lines link to different values of the equilibrium number density $\left(n_0\right)$ in non-planar (cylindrical) geometry in the classical regime ($ħ\to 0$).

Figure 12

Same as Fig. 11, but for different values of the normalized kinematic viscosity $\left({\eta }^{\ast }\right)$.

Figure 13

Same as Fig. 11, but for different values of the normalized Coriolis rotational force $\left(C_F^{\ast }\right)$.

Figure 14

Same as Fig. 11, but for different values of the normalized thermal temperature $\left(T^{\ast }\right)$. The second subplot is the magnified version depicting the peaks (kinks) clearly.

Figure 15

Same as Fig. 11, but for different values of the magnetic field $\left(B\right)$. The second subplot is the magnified version depicting the peaks (kinks) clearly.

Figure 16

Profile of the normalized growth rate $\left({\mathrm{\Omega }}_i\right)$ with variation in the normalized wavenumber $\left(k^{\ast }\right)$. The different lines link to different values of the equilibrium number density $\left(n_0\right)$ in planar (non-cylindrical) geometry in the classical regime ($ħ\to 0$). The second subplot is its enlarged version clearly showing the trends for $n_0={10}^{21}$ m^-3 and $n_0={10}^{23}$ m^-3.

Figure 17

Same as Fig. 16, but for different values of the normalized kinematic viscosity $\left({\eta }^{\ast }\right)$.

Figure 18

Same as Fig. 16, but for different values of the normalized Coriolis rotational force $\left(C_F^{\ast }\right)$.

Figure 19

Same as Fig. 16, but for different values of the normalized thermal temperature $\left(T^{\ast }\right)$. The second subplot is the magnified version depicting the peaks (kinks) clearly.

Figure 20

Same as Fig. 16, but for different values of the magnetic field $\left(B\right)$. The second subplot is the magnified version depicting the peaks (kinks) clearly.