Predictive dynamical modeling and stability of the equilibria in a discrete fractional difference COVID-19 epidemic model

Abstract

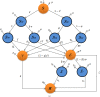
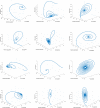
The SARSCoV-2 virus, also known as the coronavirus-2, is the consequence of COVID-19, a severe acute respiratory syndrome. Droplets from an infectious individual are how the pathogen is transmitted from one individual to another and occasionally, these particles can contain toxic textures that could also serve as an entry point for the pathogen. We formed a discrete fractional-order COVID-19 framework for this investigation using information and inferences from Thailand. To combat the illnesses, the region has implemented mandatory vaccination, interpersonal stratification and mask distribution programs. As a result, we divided the vulnerable people into two groups: those who support the initiatives and those who do not take the influence regulations seriously. We analyze endemic problems and common data while demonstrating the threshold evolution defined by the fundamental reproductive quantity $R_0$ . Employing the mean general interval, we have evaluated the configuration value systems in our framework. Such a framework has been shown to be adaptable to changing pathogen populations over time. The Picard Lindelöf technique is applied to determine the existence-uniqueness of the solution for the proposed scheme. In light of the relationship between the $R_0$ and the consistency of the fixed points in this framework, several theoretical conclusions are made. Numerous numerical simulations are conducted to validate the outcome.

Keywords: 26A33; 26A51; 26D07; 26D10; 26D15; Discrete fractional operator; Equilibrium points; Existence and uniqueness; Fractional difference equation; Local and global stability.

Fig. 1

Highly infectious individuals from June to December 2021 (see; [23]).

Fig. 2

Schematic view of COVID-19 model.

Fig. 3

Graphical view for all initial exposed peoples. It is evident that every graph leads to an EE point. This modeling was functioning. We furthermore ran a test run for a longer time frame, and the outcome was equivalent. Graphical view of (a) $\mathcal{S}$ vs. $\mathcal{E}$ (b)A phase comparison of $\mathcal{E}$ and $\mathcal{I}$.

Fig. 4

Phase portraits of EE ${\overline{E}}_1$ for various fractional-order derivatives having stability ${\mathbb{R}}_0>1$.

Fig. 5

Graphical view of the fractional-order model (11)(a) uninfected and infected class (b) time dependent graph for various compartments.

Fig. 6

Graphical view of the Covid-19 model (11)(a) the integer-order, the commensurate and the incommensurate order incorporating the real data (b) Time-dependent graph for the integer order and real data.