Mutation enhances cooperation in direct reciprocity
- PMID: 37155877
- PMCID: PMC10193978
- DOI: 10.1073/pnas.2221080120
Mutation enhances cooperation in direct reciprocity
Abstract
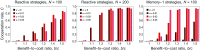
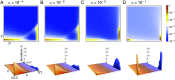
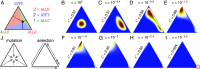
Direct reciprocity is a powerful mechanism for the evolution of cooperation based on repeated interactions between the same individuals. But high levels of cooperation evolve only if the benefit-to-cost ratio exceeds a certain threshold that depends on memory length. For the best-explored case of one-round memory, that threshold is two. Here, we report that intermediate mutation rates lead to high levels of cooperation, even if the benefit-to-cost ratio is only marginally above one, and even if individuals only use a minimum of past information. This surprising observation is caused by two effects. First, mutation generates diversity which undermines the evolutionary stability of defectors. Second, mutation leads to diverse communities of cooperators that are more resilient than homogeneous ones. This finding is relevant because many real-world opportunities for cooperation have small benefit-to-cost ratios, which are between one and two, and we describe how direct reciprocity can attain cooperation in such settings. Our result can be interpreted as showing that diversity, rather than uniformity, promotes evolution of cooperation.
Keywords: direct reciprocity; donation game; evolution of cooperation; mutation rate.
Conflict of interest statement
The authors declare no competing interest.
Figures
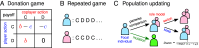

References
-
- Skyrms B., Evolution of the Social Contract (Cambridge University Press, 2014).
-
- Trivers R. L., The evolution of reciprocal altruism. Q. Rev. Biol. 46, 35–57 (1971).
-
- Axelrod R., The Evolution of Cooperation (Basic Books, New York, NY, 1984).
-
- Boyd R., Lorberbaum J., No pure strategy is evolutionary stable in the iterated prisoner’s dilemma game. Nature 327, 58–59 (1987).
Publication types
MeSH terms
Associated data
LinkOut - more resources
Full Text Sources
Miscellaneous

