On the combinatorics of crystal structures. II. Number of Wyckoff sequences of a given subdivision complexity

Abstract

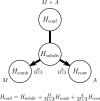
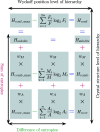
Wyckoff sequences are a way of encoding combinatorial information about crystal structures of a given symmetry. In particular, they offer an easy access to the calculation of a crystal structure's combinatorial, coordinational and configurational complexity, taking into account the individual multiplicities (combinatorial degrees of freedom) and arities (coordinational degrees of freedom) associated with each Wyckoff position. However, distinct Wyckoff sequences can yield the same total numbers of combinatorial and coordinational degrees of freedom. In this case, they share the same value for their Shannon entropy based subdivision complexity. The enumeration of Wyckoff sequences with this property is a combinatorial problem solved in this work, first in the general case of fixed subdivision complexity but non-specified Wyckoff sequence length, and second for the restricted case of Wyckoff sequences of both fixed subdivision complexity and fixed Wyckoff sequence length. The combinatorial results are accompanied by calculations of the combinatorial, coordinational, configurational and subdivision complexities, performed on Wyckoff sequences representing actual crystal structures.

Keywords: Shannon entropy; Wyckoff sequences; combinatorics; structural complexity.

Figure 1

Geometric interpretation for the problem of finding the number of ways of combining individual Wyckoff positions of given multiplicities and arities, , adding up to a given total multiplicity and arity . In the illustration, the target vector , here written in row form, is denoting a point in the two-dimensional integer lattice (square lattice) in the upper-right corner. On the top, the individual vectors corresponding to each Wyckoff position are shown: a (2,0) red, b (2,0) green, c (2,1) blue, d (4,1) dark red, e (4,2) dark green, f (8,3) dark blue. On the bottom, their combinations adding up to are shown, with vectors composed in reverse lexicographic order. Other possible combinations, in which only the order of the vectors are changed, are not shown. However, all lattice points which can be reached by any possible combinations of vectors are highlighted as open circles instead of filled ones. To see the full graph one has to invert the depicted half of it in the point (6, 1.5). In this interpretation the problem becomes a special case of a lattice path enumeration problem with the set of steps governed by the Wyckoff multiplicities and arities for a given choice of space-group symmetry.

Figure 2

Dynamic programming algorithm (given in pseudocode) for the determination of the number of Wyckoff sequences of a given space group and subdivision complexity as determined by the total number of degrees of freedom for the Wyckoff multiplicity and arity (bivariate case).

Figure 3

Dynamic programming algorithm (given in pseudocode) for the determination of the number of Wyckoff sequences of a given space group, subdivision complexity and length as determined by the total number of degrees of freedom for the Wyckoff multiplicity, Wyckoff arity and length (trivariate case). Note that for all Wyckoff sites – this does not have to be specified for each Wyckoff position independently. However, possible simplifications due to this fact have not been included in the pseudocode in order to highlight its similarity with the bivariate case shown in Fig. 2 ▸.

Figure 4

Schematic representation of the relation between the configurational complexity , calculated for degrees of freedom, and the combinatorial and coordinational complexities, and , calculated for M and A degrees of freedom, respectively. Shown also are the weighting factors and as well as the unit weight contribution of the invariant subdivision complexity which taken all together sum to the configurational complexity . For a given choice of M and A the subdivision complexity is a constant, while the combinatorial and coordinational complexities, and , depend on the respective partitions of M and A possible for a given space-group type.

Figure 5

Schematic representation of the interrelation between various maximal and non-maximal entropies (combinatorial, coordinational, configurational) and the subdivision entropy on different levels of structural hierarchy. On the Wyckoff position level of hierarchy the difference of (maximal) entropies defines the conventional non-maximal entropies (from left to right), while on the crystal structure level of hierarchy the (partially weighted) sum of entropies defines the maximal and non-maximal configurational entropy (from bottom to top). Note that the distinction between differences and sums of entropies depends on a deliberate choice of how to distribute terms on either side of the equals sign. In the scheme as presented here, the case for differences of entropies is based on the choice of collecting all maximal entropies together, while distributing collective and individual contributions on opposite sides of the equation could highlight the fact that the non-maximal entropies fulfil the same role as a subdivision complexity on the Wyckoff position level as the subdivision complexity does on the crystal structure level, thus highlighting the applicability of the strong additivity property on both levels of hierarchy (in this case the common weighting factors or can be omitted on the Wyckoff position level of hierarchy).

Figure 6

Generating polynomial approach (Mathematica).

Figure 7

Dynamic programming approach (Python). Here, the target tuple is given as and the Wyckoff tuples are given as .