Contributions of global and local processing on medical image perception

Abstract

Purpose: The influential holistic processing hypothesis attributes expertise in medical image perception to cognitive processing of global gist information. However, it has remained unclear whether or how experts use rapid global impression of images for their subsequent diagnostic decisions based on the focal sign of cancer. We hypothesized that continuous-global and discrete-local processes jointly attribute to radiological experts' detection of mammogram, with different weights and temporal dynamics.

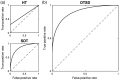
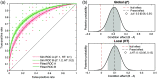
Approach: We examined experienced versus inexperienced observers' performance at first (500 ms) versus second (2500 ms) mammogram image presentation in an abnormality detection task. We applied a dual-trace signal detection (DTSD) model of receiver operating characteristic (ROC) to assess the time-varying contributions of global and focal cancer signals on mammogram reading and medical expertise.

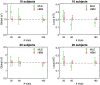
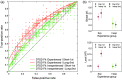
Results: The hierarchical Bayesian DTSD modeling of empirical ROCs revealed that mammogram expertise (experienced versus inexperienced observers) manifests largely in a continuous-global component for the detection of the gist of abnormality at the early phase of mammogram reading. For the second presentation of the same mammogram images, the experienced participants showed increased task performance that was largely driven by better processing of discrete-local information, whereas the global processing of abnormality remained saturated from the first exposure. Modeling of the mouse trajectory of the confidence rating responses further revealed the temporal dynamics of global and focal processing.

Conclusions: These results suggest a joint contribution of continuous-global and discrete-local processes on medical expertise, and these processes could be analytically dissociated.

Keywords: focal process; hierarchical Bayesian; holistic process; mammography; mouse trajectory; signal detection.

Fig. 1

Mammogram abnormality detection task. Each trial began with an 800-ms central fixation, followed by the first mammogram image presentation at the center of the screen for 500 ms (short-first). After image offset, participants reported whether the image is normal or abnormal along with the level of confidence by clicking the mouse cursor on the continuous confidence scale presented on the right side of the screen. Mouse trajectory was recorded. After the first response, the same image was presented for 2500 ms (long-second) and participants again reported the abnormality and confidence.

Fig. 2

DTSD model. (a) The main idea of the DTSD model is that the curvilinear and asymmetrical ROCs (b) observed from diagnostic medical decisions can be modeled as a mixture of two distinct components: (1) high-threshold component (HT, top-left) for the discrete-local processing of focal signs of abnormality (e.g., identification of malignant lesions) manifests as linear ROCs. (2) SDT component ($d^{\prime }$, bottom-left) for the continuous-global processing of the gist of abnormality (e.g., observer’s prior knowledge about the visual patterns of abnormal images) manifest as symmetrical and curvilinear ROCs.

Fig. 3

Recovery of the DTSD model parameters as a function of the number of subjects and trials, using fixed parameter values: global $(d^{\prime })=1.5$, and local (HT) = 0.2. The parameters were estimated under HBM and MLE methods for the same set of simulated ROCs. Green data points on this figure represent the means and the ${\mathrm{CI}}_{95\%}$ of the individual subject. Red data points represent the means and the ${\mathrm{HDI}}_{95\%}$ of the population-level parameter posteriors. The dashed-line represents the true parameter values used for data simulation.

Fig. 4

Recovery of the condition effect in the DTSD model parameters by the HBM method. ROCs were simulated separately for two hypothetical conditions: for condition A, global $(d^{\prime })=1.0$, local (HT) = 0.1; for condition B, global $(d^{\prime })=1.2$, local (HT) = 0.2. The condition effect (condition B to A) is thus defined as $\mathrm{\Delta }{d}^{\prime }=0.2$ and $\mathrm{\Delta }\mathrm{HT}=0.1$, respectively. Forty trials (20 target and 20 nontarget trials) for each of 13 subjects per condition were simulated. (a) The simulated (dotted-line) and (b) recovered (solid-line) ROC curves. The shaded error bars indicate the 95% ${\mathrm{CI}}_{95\%}$ of the recovered ROCs across subjects. Red and green colors represent condition A and B, respectively. Dots on this figure are simulated data points across subjects and confidence rating bins. (b) The recovered condition effect represented on the posterior probability functions of the group-level DTSD model parameters. The circle markers and the gray areas represent the means and the ${\mathrm{HDI}}_{95\%}$ of the population-level parameter posteriors (values shown in the legend). The black and red dashed-lines represent the preset condition effect and the null effect, respectively.

Fig. 5

(a) Observed ROCs as a function of radiological experience (experienced versus inexperienced) and image exposure duration (short-first versus long-second), overlapped with the hierarchical Bayesian DTSD model fits (solid lines). The horizontal and vertical error bars indicate standard errors of false alarm (FA) rates and hit rates, respectively. The small dots indicate individual data points across participants and 19-bins confidence ratings. (b) The means and the ${\mathrm{HDI}}_{95\%}$ of posteriors of the population-level hierarchical Bayesian DTSD model parameters, global ($d^{\prime }$) and local (HT), as a function of experience group and image exposure duration.

Fig. 6

Mean mouse trajectories on a half-circle confidence rating scale as a function of radiological experience group (experienced versus inexperienced), pathology (normal versus abnormal), and image exposure duration (short-first versus long-second). From the central line on the scale, counterclockwise and clockwise areas correspond to normal and abnormal ratings along the continuous confidence scale from guess, probably, and sure. Error bars represent standard error of means for horizontal mouse cursor positions from movement onset to final click.

Fig. 7

A 2D histogram depicting standardized group-aggregated mouse trajectory destination-vector distributions as a function of confidence rating ($x$ axis), normalized time ($y$ axis), and $z$-scored probability ($z$ axis). A three-way interaction effect in mouse trajectory data: radiological experience group × pathology × image exposure duration, illustrating how the radiological expertise effect (experienced–inexperienced) in detecting the abnormality signal over noise (abnormal–normal) emerged differently between short- and long-image exposure durations (long-second to short-first). Since the effect plotted includes the difference between pathology condition (i.e., abnormal to normal), the probabilities on the right side from the midline indicate “hit rate–FA rate,” whereas the left side from the midline indicate “miss rate–correct rejection (CR) rate,” respectively. The dotted-contours on the histogram denote the areas of probability exceeding $\pm 1.96$ $z$-score (sd) of the three-way interaction effect.

Fig. 8

Aggregated raw mouse trajectory destination-vector distributions for each combination of radiological experience (experienced versus inexperienced), pathology (normal versus abnormal), and image exposure duration conditions (short-first versus long-second). For the normal image conditions, the probabilities on the left (toward normal) and right side (toward abnormal) of the midline indicate CR and FA responses, respectively. For the abnormal image conditions, the probabilities on the left and right side of the midline indicate miss and hit responses, respectively.