Modified conformable double Laplace-Sumudu approach with applications

Abstract

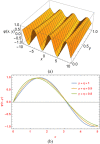
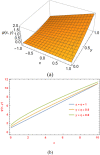
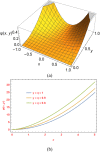
In this study, we combine two novel methods, the conformable double Laplace-Sumudu transform (CDLST) and the modified decomposition technique. We use the new approach called conformable double Laplace-Sumudu modified decomposition (CDLSMD) method, to solve some nonlinear fractional partial differential equations. We present the essential properties of the CDLST and produce new results. Furthermore, five interesting examples are discussed and analyzed to show the efficiency and applicability of the presented method. The results obtained show the strength of the proposed method in solving different types of problems.

Keywords: Conformable derivative; Decomposition method; Double laplace– sumudu transform; Laplace transform; Sumudu transform.

Fig. 1

(a) The 3D plots of the solution of Equation (30) gained by the presented method comparing to the exact solution, (b) The CDLSMD solution of $\psi \left(\frac{{\mathcal{x}}^{\eta }}{\eta },\frac{{\mathcal{y}}^{\gamma }}{\gamma }\right)$ for Equation (30) at $\eta =\gamma =\mathrm{1,0.9,0.8}$.

Fig. 2

(a) The 3D plots solution of Equation (36) gained using the presented method comparing to the exact solution (b) The CDLSMD solution of $\psi \left(\frac{{\mathcal{x}}^{\eta }}{\eta },\frac{{\mathcal{y}}^{\gamma }}{\gamma }\right)$ for Equation (36) at $\eta =\gamma =\mathrm{1,0.9,0.8}$.

Fig. 3

(a) The 3D plots of the solution graph of Equation (41) gained by the presented technique comparing with accurate solution (b) The CLSMD solution of $\psi \left(\frac{{\mathcal{x}}^{\eta }}{\eta },\frac{{\mathcal{y}}^{\gamma }}{\gamma }\right)$ for Equation (41) at $\eta =\gamma =\mathrm{1,0.9,0.8}$.

Fig. 4

(a) The 3D solution graphs of Equation (47) obtained by the presented method comparison with exact solution (b) The CDLSMD solution of $\psi \left(\frac{{\mathcal{x}}^{\eta }}{\eta },\frac{{\mathcal{y}}^{\gamma }}{\gamma }\right)$ for Equation (47) at $\eta =\gamma =\mathrm{1,0.9,0.8}$.

Fig. 5

(a) The 3D plots of the solution of Equation (53) gained by the presented method comparing to the exact solution (b) The CDLSMD solution of $\psi \left(\frac{{\mathcal{x}}^{\eta }}{\eta },\frac{{\mathcal{y}}^{\gamma }}{\gamma }\right)$ for Equation (53) at $\eta =\gamma =\mathrm{1,0.9,0.8}$.