Skip to main page content
U.S. flag

An official website of the United States government

Dot gov

The .gov means it’s official.
Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.

Https

The site is secure.
The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.

Access keys NCBI Homepage MyNCBI Homepage Main Content Main Navigation
. 2023 May 1;23(9):4442.
doi: 10.3390/s23094442.

Multi-Harmonic Modulation in a Fiber-Optic Gyroscope

Martin Miranda  1 , Nobuyuki Takei  1   2 , Yuki Miyazawa  1 , Mikio Kozuma  1   3
Affiliations

Multi-Harmonic Modulation in a Fiber-Optic Gyroscope

Martin Miranda et al. Sensors (Basel). .

Abstract

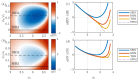
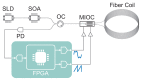
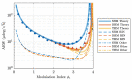
Optimizing the bias modulation of a fiber-optic gyroscope is crucial to improving its precision. In this study, we propose and demonstrate the use of multiple harmonics of sinusoidal modulation as an intermediate alternative to the widely used modulation methods: sinusoidal and square-wave modulation. We show that this alternative integrates the advantages of each modulation method by providing a smooth modulation that produces a clean, spike-free output and a satisfactory signal-to-noise ratio. By using three harmonics of modulation in combination with a high frequency to reduce thermal phase noise, we obtained an angular random walk of 5.2(2)μdeg/h and a bias instability of ∼10μdeg/h. This is the highest performance ever reported for fiber-optic gyroscopes.

Keywords: fiber-optic gyroscope; multiple harmonics; relative-intensity noise; sinusoidal bias modulation; thermal-phase noise.

PubMed Disclaimer

Conflict of interest statement

The authors declare no conflict of interest.

Figures

Figure 1
Figure 1
Improvement of RIN- and SN-induced ARW for multi-harmonic modulation. Improvement units are in dB. (a,b): ηRIN and ηSN as a function of ϕ1 and ratio ϕ3/ϕ1. SHM and optimal DHM ratios ϕ3/ϕ1 are shown as solid and dashed lines, respectively. (c) ηRIN as a function of ϕ1 for fixed ratios: ϕ3/ϕ1=0.234 for DHM; ϕ3/ϕ1=0.288 and ϕ5/ϕ1=0.118 for THM. (d) ηSN as a function of ϕ1 for fixed ratios: ϕ3/ϕ1=0.188 for DHM; ϕ3/ϕ1=0.235 and ϕ5/ϕ1=0.080 for THM. For comparison, the SWM case is shown as a function of 4ϕ/π in (c,d).
Figure 2
Figure 2
Schematic setup of the experimental apparatus. SLD, super-luminescent diode; SOA, semiconductor optical amplifier; OC, optical circulator; MIOC, multifunctional integrated optical chip; PD, photodetector.
Figure 3
Figure 3
ARW dependence on the modulation index ϕ1 for SHM, DHM (ϕ3/ϕ1=0.234) and THM ((ϕ3,ϕ5)/ϕ1=(0.288,0.118)) denoted by circular, triangular and square points, respectively. Solid lines: Total estimated ARW including all sources of noise. Dashed lines: RIN-induced ARW. Dashed-dotted lines: SN-, DN- and TPN-induced ARW.
Figure 4
Figure 4
Modulation frequency dependency of the ARW for the SHM case. Solid dots: Experimental results. Solid line: ARW including all sources of noise. Dashed line: TPN contribution to ARW. Dashed-dotted lines: Sum of other noise-induced ARW, including SN, DN and RIN.
Figure 5
Figure 5
Allan deviation for 12-hour measurements of SHM, DHM, and THM.
Figure 6
Figure 6
Dependence of the ARW on the number of modulation harmonics. The dashed line shows the best ARW attainable using ideal square-wave modulation.
See this image and copyright information in PMC

References

    1. Léfevre H.C., Steib A., Claire A., Sekeriyan A., Couderette A., Pointel A.L., Viltard A., Bonnet A., Frénois A., Gandoin A., et al. The fiber optic gyro ’adventure’ at Photonetics, iXsea and now iXblue. In: Lieberman R.A., Sanders G.A., Scheel I.U., editors. Proceedings of the Optical Waveguide and Laser Sensors; Online. 27 April–8 May 2020; Bellingham, WA, USA: International Society for Optics and Photonics; 2020. p. 1140505. - DOI
    1. Song N., Xu X., Zhang Z., Gao F., Wang X. Advanced Interferometric Fiber Optic Gyroscope for Inertial Sensing: A Review. J. Light. Technol. 2023:1–14. doi: 10.1109/JLT.2023.3260839. - DOI
    1. Lefevre H.C. The Fiber-Optic Gyroscope. Artech House; Norfolk County, MA, USA: 2022.
    1. de Toldi E., Lefèvre H., Guattari F., Bigueur A., Steib A., Ponceau D., Moluçon C., Ducloux E., Wassermann J., Schreiber U. First steps for a Giant FOG: Searching for the limits; Proceedings of the 2017 DGON Inertial Sensors and Systems (ISS); Karlsruhe, Germany. 19–20 September 2017; pp. 1–14. - DOI
    1. Schmelzbach C., Donner S., Igel H., Sollberger D., Taufiqurrahman T., Bernauer F., Häusler M., Renterghem C.V., Wassermann J., Robertsson J. Advances in 6C seismology: Applications of combined translational and rotational motion measurements in global and exploration seismology. Geophysics. 2018;83:WC53–WC69. doi: 10.1190/geo2017-0492.1. - DOI

LinkOut - more resources