Nonlinear propagation of quasiplanar shear wave beams in soft elastic media with transverse isotropy

Abstract

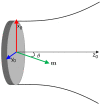
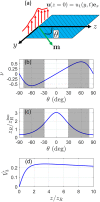
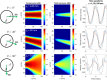
Model equations are developed for shear wave propagation in a soft elastic material that include effects of nonlinearity, diffraction, and transverse isotropy. A theory for plane wave propagation by Cormack [J. Acoust. Soc. Am. 150, 2566 (2021)] is extended to include leading order effects of wavefront curvature by assuming that the motion is quasiplanar, which is consistent with other paraxial model equations in nonlinear acoustics. The material is modeled using a general expansion of the strain energy density to fourth order in strain that comprises thirteen terms defining the elastic moduli. Equations of motion for the transverse displacement components are obtained using Hamilton's principle. The coupled equations of motion describe diffraction, anisotropy of the wave speeds, quadratic and cubic plane wave nonlinearity, and quadratic nonlinearity associated with wavefront curvature. Two illustrative special cases are investigated. Spatially varying shear vertical wave motion in the fiber direction excites a quadratic nonlinear interaction unique to transversely isotropic soft solids that results in axial second harmonic motion with longitudinal polarization. Shear horizontal wave motion in the fiber plane reveals effects of anisotropy on third harmonic generation, such as beam steering and dependence of harmonic generation efficiency on the propagation and fiber directions.

FIG. 1.

(Color online) Schematic diagram of the reference frame. Quasiplanar SH and SV waves are polarized at leading order in the x₀ (red) and y₀ (blue) directions, respectively, and the fiber direction (green) lies in the y₀-z₀ plane according to Eq. (5). Wave motion is generated by a source at $z_0=0$ that has finite extent in the x₀-y₀ plane.

FIG. 2.

(Color online) Schematic of the source motion for the special case analyzed in Sec. IV.

FIG. 3.

(Color online) Amplitudes of the three harmonic components in the longitudinally polarized field along the beam axis, obtained numerically using Eqs. (50)–(53) with $N_2=0.2,\hspace{0.17em}{N}_3=0.3$, and ka = 20, and for the source condition given by Eq. (54) with m = 1 (upper row) and m = 4 (lower row).

FIG. 4.

(Color online) (a) Schematic representation of the example investigated in Sec. V, showing source motion (red arrows) and fiber direction (green arrow). (b) Beam steering parameter ν versus fiber direction θ. (c) Ratio of anisotropic diffraction length to the isotropic diffraction length. Grey regions in (b) and (c) indicate fiber directions for which beam steering renders the paraxial approximation invalid. Parameters used in (b) and (c) are for in vivo human thigh: (Ref. 23) $\mu =1.9$ kPa, ${\alpha }_1=19.7$ kPa, and ${\alpha }_2=7.8$ kPa. (d) Third harmonic amplitude ${\widehat{V}}_3=|V_3(y=\nu z)|/(k_1{z}_R{\beta }_1{v}_0^3/4c_1^2)$ along the beam axis $y=\nu z$.

FIG. 5.

(Color online) Numerical solution of Eq. (59) for propagation direction at 0°, 20°, and 90° relative to the fiber direction m. Linear material parameters are for human thigh (Ref. 23) and the coefficient of nonlinearity is ${\beta }_1=2$. Source parameters used are frequency 200 Hz, width a = 13 mm, and amplitude $v_0=250$ mm/s. Time waveforms in the right-most column are located along the beam axis at $y=\nu z$.